Uge 1: Kontinuitet

Uge 1: Kontinuitet#

Nøglebegreber#

  • Skalar-funktioner: specielt kvadratiske former

  • Vektor-funktioner

  • Visualisering af funktioner: Grafer og niveaukurver/mængder

  • Kontinuitet

  • Det sædvanlige indreprodukt (prikproduktet) og norm i \(\mathbb{R}^n\)

  • Partielle afledte og Gradientvektoren

Forberedelse og pensum#

Opgaver – Store Dag#

1: Funktion eller ej?#

Betragt følger korrespondance mellem \(a\) og \(b\) værdier:

\(a\)

\(b\)

1

0

2

1

0

3

1

2

Vi betragter funktioner hvis definitionsmængde (domain) er en delmængde af \(\{0,1,2,3\}\) og hvis dispositionsmængde (co-domain) er \(\{0,1,2,3\}\). Vi skal bestemme om \(f\) og \(g\) definerer funktioner, hvis vi lader \(f\) følge reglen at første søjle (\(a\)-værdierne) er input og anden søjle (\(b\)-værdierne) skal være output af funktionen \(f\) og definitionsmængden er \(\{0,1,2\}\); og vi lader \(g\) følge reglen om at anden søjle er input og første søjle skal være output af funktionen \(g\) med definitionsmængde \(\{0,1,2,3\}\).

Definerer \(f\) en funktion? Gør \(g\)? I bekræftende fald: bestem værdimængden/billedmængden (engelsk: range/image) for funktionen, og afgør om funktionen er injektiv og surjektiv.

Hint

Læs dette afsnit i noten

Svar

Kun \(g\) er en funktion, da \(f\) både forsøger at definere \(f(1)=0\) og \(f(1)=2\). Funktionen \(g\) har \(\mathrm{im}(g) = \{0,1,2,\} \subset \{0,1,2,3\}\) er derfor ikke surjektiv. Da \(g(0)=1\) og \(g(2)=1\) er den heller ikke injektiv.

2: Ens funktionsforskrifter?#

Vi betragter funktioner \(f_i : \mathbb{R} \to \mathbb{R}\) givet ved:

\[\begin{gather*} f_1(x) = |x| \\ f_2(x) = \begin{cases} x & x > 0 \\ -x & x \le 0 \end{cases} \\ f_3(x) = \max(x,0) \\ f_4(x) = ReLU(x) + ReLU(-x) \end{gather*}\]

hvor \(x \in \mathbb{R}\).

Nogle af funktionerne er samme funktion. Find dem alle!

Hint

ReLU er defineret i noterne.

Hint

Find først \(f_i(x)\) for de forskellige funktioner for et par forskellige værdier af \(x\).

3: Mulige visualiseringer#

Diskuter om man kan visualisere nedenstående funktioner – i givet fald plot dem med SymPy/dtumathtools:

  1. En skalarfunktion af to variable \(f: \mathbb{R}^2 \to \mathbb{R}, \, f(x_1,x_2) = \sqrt{\vert x_1 x_2 \vert}\)

  2. En skalarfunktion af fire variable \(f: \mathbb{R}^4 \to \mathbb{R}, \, f(x_1,x_2,x_3,x_4) = \sqrt{\vert x_1 x_2 x_3 x_4 \vert}\)

  3. En kompleks skalarfunktion af to variable \(f: \mathbb{R}^2 \to \mathbb{C}, \, f(x_1,x_2) = \sqrt{\vert x_1 x_2 \vert} + i \cos(x_1 + x_2)\)

  4. Et vektorfelt i 2D \(\pmb{f}: \mathbb{R}^2 \to \mathbb{R}^2, \, \pmb{f}(x_1,x_2) = (-x_2/3, x_1/3)\)

  5. Et vektorfelt i 3D \(\pmb{f}: \mathbb{R}^3 \to \mathbb{R}^3, \, \pmb{f}(x,y,z)= (x^3+yz^2, y^3-xz^2, z^3)\)

  6. En funktion af formen \(\pmb{r}: [0,10] \to \mathbb{R}^3, \, \pmb{r}(t) = (\cos(t),\sin(t),t)\)

Note

Følgende Python kommandoer kan være nyttige: dtuplot.plot3d, dtuplot.plot_vector, dtuplot.plot3d_parametric_line.

Hint

Når man plotter et vektorfelt, kan det være nødvendigt at skalere vektorerne (hvis de er for korte eller lange). Dette kan gøres ved at gange vektorfeltet igennem med en skalar, fx 0.1 * f i stedet for f.

4: Forskellige(?) kvadratiske former#

Lad \(\pmb{x} = [x_1,x_2]^T\) være en søjlevektor i \(\mathbb{R}^2\). Definer:

\[\begin{equation*} A_1 =\left[\begin{matrix}11 & -12 \\ -12 & 4\end{matrix}\right], \, A_2 =\left[\begin{matrix}11 & 0 \\ -24 & 4\end{matrix}\right], \, A_3 =\left[\begin{matrix} 73/5 & -36/5 \\ -36/5 & 52/5 \end{matrix}\right], \, \end{equation*}\]

og

\[\begin{equation*} \pmb{b}_1 = \left[\begin{matrix}-20\\ 40\end{matrix}\right], \, \pmb{b}_2 = \pmb{b}_1, \, \pmb{b}_3 = \left[\begin{matrix}-44\\ 8\end{matrix}\right], \, c = -60 \end{equation*}\]

Lad \(q_i: \mathbb{R}^2 \to \mathbb{R}\) være givet ved:

\[\begin{equation*} q_i(\pmb{x}) = \pmb{x}^T A_i \pmb{x} + \pmb{b}_i^T \pmb{x} + c \end{equation*}\]

for \(i=1,2,3\). Sådanne funktioner kaldes kvadratiske former, se denne definition.

Spørgsmål a#

Gang udtrykket for \(q_1(x_1,x_2)\) ud. Først i hånden, så ved hjælp af Python. Gang også udtrykkene for \(q_2(x_1,x_2)\) og \(q_3(x_1,x_2)\) (i hånden eller Python) ud.

Hint

Det kan være nødvendigt at bruge c = Matrix([-60]) da SymPy ikke vil lægge skalarer sammen med 1x1 matricer. Omvendt, kan en 1x1 SymPy matrix q1 laves om til en skalar ved enten q1[0,0] eller q1[0].

Svar

\( q_1(\pmb{x}) = 11 x_{1}^{2} - 24 x_{1} x_{2} - 20 x_{1} + 4 x_{2}^{2} + 40 x_{2} - 60\)

Spørgsmål b#

Er den kvadratiske matrix \(A\) i en kvadratisk form (som fx \(\pmb{x}^T A \pmb{x}\)) entydig givet?

Hint

Kig på \(q_1(\pmb{x})\) og \(q_2(\pmb{x})\)

Svar

Nej. Fx er \(q_1(\pmb{x}) = q_2(\pmb{x})\), mens \(A_1 \neq A_2\).

Spørgsmål c#

Plot grafen af funktionen \(q_1\). Plot så nogle niveaukurver. Hvilken geometrisk form har niveaukurverne? Gør det samme for \(q_3\).

Spørgsmål d#

En af funktionerne har et minimum. Hvilken? Hvor ligger det cirka? Hvad kaldes det samme punkt for de funktioner der ikke har et minimum?

Svar

  • \(q_3\) har et minimum

  • Det ligger i \((2,1)\) (det skal bare aflæses fra et plot)

  • \(q_1\) har et såkaldt saddelpunkt i samme punkt, Wikipedia

5: lineær vektor-funktion#

Lad \(A \in \mathsf{M}_{3 \times 5}(\mathbb{R})\) være givet ved

\[\begin{equation*} A = \begin{bmatrix} 1 & 0 & 2 & 3 & 4 \\ 0 & -1 & 5 & 6 & 7 \\ 0 & 0 & -3 & 8 & 9 \end{bmatrix} \end{equation*}\]

Betragt vektorfunktionen \(\pmb{f}: \mathbb{R}^5 \to \mathbb{R}^3\) givet ved \(\pmb{f} = \pmb{x} \mapsto A\pmb{x}\), hvor \(\pmb{x}\) er en søjlevektor i \(\mathbb{R}\).

Spørgsmål a#

Angiv de 3 koordinatfunktioner for \(\pmb{f}\).

Hint

Husk at koordinatfunktionerne \(f_i\) er \(\pmb{f} = (f_1,f_2,f_3)\).

Spørgsmål b#

Angiv billedmængden \(\mathrm{im}(\pmb{f})\) for \(\pmb{f}\).

Hint

Hvad er rangen af \(A\)? Hvad er søjlerummet (column space \(\mathrm{col}A\)) af \(A\)?

Svar

\(\mathrm{im}(\pmb{f}) = \mathrm{col}A = \mathbb{R}^3 \)

Spørgsmål c#

Er vektorfunktionen \(\pmb{f}\) surjektiv og/eller injektiv?

Svar

\(\pmb{f}\) er surjektiv, da \(\mathrm{im}(\pmb{f}) = \mathbb{R}^3\). Den er ikke injektiv, da \(\mathrm{dim \, ker}(A) = 5-3=2\) (du bør finde to forskellige vektorer \(\pmb{x}_1, \pmb{x}_2 \in \mathbb{R}^5\) for hvilke \(\pmb{f}(\pmb{x}_1) = \pmb{f}(\pmb{x}_2)\)).

6: Størrelse af vektorer#

Betragt følgende tre vektorer i \(\mathbb{R}^3\):

\[\begin{equation*} \pmb{v}_1 = \left[\begin{matrix}-10\\ -10\\ -10\end{matrix}\right], \, \pmb{v}_2 = \left[\begin{matrix}-10\\ -4\\ 14\end{matrix}\right], \, \pmb{v}_3 = \left[\begin{matrix}-10\\ -8\\-12\end{matrix}\right] \end{equation*}\]

Hvilken vektor er længst? Hvilke vektorer er ortogonale på hinanden? Hvilke to vektorer er tættest på hinanden?

Note

Vi kan forestille os vektorerne som (geometriske) stedvektorer med begyndelsespunkt i \(\pmb{0}=[0,0,0]^T\) og slutpunkt \(\pmb{v}_i\) for hhv \(i=1,2,3\). Under tiden skriver man dette som \(\overrightarrow{\pmb{0}\pmb{v}_i}\).

7: Chatbots og (dis-)kontinuitet#

Spørg en chatbot, fx BingChat, Open IAs ChatGPT eller Microsoft Copilot, om den kan give et eksempel på en funktion \(f: \mathbb{R} \to \mathbb{R}\), der er kontinuert i præcis 3 punkter og diskontinuert i alle andre punkter. Vurdér om chatbottens svar er korrekt eller forkert. Kan man plotte funktionen fra chatbottens eksempel?

8: Python-funktion som matematisk funktion#

Betragt følgende funktion:

from sympy import *
from dtumathtools import *
init_printing()

def f(x1,x2):
    return Matrix([ln(x1), x1 * x2**2 + 1])

Note

Man kan definere den samme funktion med følgende en-linjes kald: myfun = lambda x1,x2: Matrix([ln(x1), x1 * x2**2 + 1]). Der er Python-tekniske forskelle på de to metoder, men i brug minder de meget om hinanden. Vi anbefaler generelt at der bruges def-funktioner. Lambda-funktioner er dog brugbare i situationer hvor funktionen kun skal bruges én gang og i kald til andre funktioner, fx sorted(['a1', 'z0'], key = lambda x: int(x[1])).

Note

  • Det er ikke nødvendigt at definere x1,x2 = symbols("x1 x2")

  • Selv om vi tit arbejder med funktioner i dette kursus, så er det ofte ikke nødvendigt at definere Python-funktioner, fx findes den afledte af \(f(x)=x^2 \cos(x)\) jo blot ved:

x = symbols("x")
f = x**2 * cos(x)
f.diff()

Spørgsmål a:#

Hvad er funktionsværdien i \(f(2,-3)\)?

Spørgsmål b:#

Skriv Python-funktionen ned som en matematisk funktion. Dispositionsmængden (co-domain) er \(\mathbb{R}^2\). Hvad er definitionsmængden (domain)?

Hint

I Python skal man ikke angive “definitionsmængder”. Vi mener derfor her at definitionsmængden skal være den størst mulige.

Hint

Hvad er definitionsmængden for logaritmen?

Svar

\(\mathrm{dom}(f) = ]0,\infty [ \times \mathbb{R}\)

Spørgsmål c:#

Find billedmængden (engelsk: image/range).

Hint

Spørgsmålet er for hvilke \((y_1, y_2) \in \mathbb{R}^2\), ligningerne \(y_1 = \ln(x_1)\) og \(y_2 = x_1 \, x_2^2 + 1\) har en løsning. Kig først på ligningen \(y_1 = \ln(x_1)\).

Hint

Hvis \(x_1\) kun kan være et vilkårligt positivt, reelt tal, hvilke værdier kan \(x_1 \, x_2^2 + 1\) så antage?

Svar

\(\mathrm{im} (f) = \mathbb{R} \times [1, \infty [\)

9: Kontinuitet af førstegradspolynomier#

Bevis at polynomiumsfunktionen \(f : \mathbb{R} \to \mathbb{R}\), \(f(x)=3x\) er kontinuert i alle punkter \(x \in \mathbb{R}\).

Hint

Brug \(\epsilon-\delta\) definitionen. Se denne ligning i noten.

Hint

Lad \(x_0\) være et vilkårligt reelt tal, og lad \(\epsilon > 0\) være givet. Du skal nu angive hvordan man kan vælge \(\delta > 0\) (det må gerne afhænge af \(x_0\) og \(\epsilon\)) så \( |x-x_0| < \delta \Rightarrow |f(x)-f(x_0)| < \epsilon\).

Opgaver – Lille Dag#

1: Partielle afledede af simpel skalar-funktion#

Find de partielle afledte \(\frac{\partial f}{\partial x_1}\) og \(\frac{\partial f}{\partial x_2}\) for \(f(x_1, x_2) = x_1^3 + 3x_1 x_2 + x_2^3\). Bestem værdien af de partielle afledte i punktet \((x_1,x_2)=(1,2)\).

Hint

  • Husk formlen for partielle afledte med hensyn til hver variabel.

  • Behandl andre variable som konstanter under differentiering.

Svar

  • \(\frac{\partial f}{\partial x_1} = 3x_1^2 + 3x_2\)

  • \(\frac{\partial f}{\partial x_2} = 3x_2^2 + 3x_1\)

  • I punktet \((1,2)\): \(\frac{\partial f}{\partial x_1}(1, 2) = 9\), \(\frac{\partial f}{\partial x_2}(1, 2) = 15\)

2: Kvadratiske former med symmetriske matricer#

Lad \(A\) være en vilkårlig \(n \times n\) matrix, og lad \(\pmb{x}\) være en søjlevektor i \(\mathbb{R}^n\). Definer \(B\) ved \(B = (A + A^T)/2\).

Spørgsmål a#

Vis at matricen \(B\) er symmetrisk

Hint

En matrix \(B\) er symmetrisk hvis og kun hvis \(B = B^T\). Husk at \(B = \tfrac{1}{2} (A + A^T) \)

Svar

\( B^T = ((A + A^T)/2)^T = \tfrac{1}{2} (A^T + (A^T)^T) = \tfrac{1}{2} (A^T + A) = \tfrac{1}{2} (A + A^T) = B \)

Spørgsmål b#

Vis at \(\pmb{x}^T A \pmb{x} = \pmb{x}^T B \pmb{x}\).

Spørgsmål c#

Konkludér at man altid kan antage at kvadratiske former af formen \(q(\pmb{x}) = \pmb{x}^T A \pmb{x} + \pmb{b}^T \pmb{x} + c\) er givet ved en symmetrisk matrix \(A\).

3: Niveaukurver og gradienter#

Vi betragter funktion \(f:\mathbb{R}^2\rightarrow \mathbb{R}\) givet ved forskriften

\[\begin{equation*} f(x,y)=x^2-2y \end{equation*}\]

og dens niveaukurver

\[\begin{equation*} f(x,y)=c,\, c\in\mathbb{R} \end{equation*}\]

Spørgsmål a#

Vis at niveaukurven for et vilkårligt \(c\) kan beskrives ved en ligning på formen \(y=g_c(x)\) hvor \(g_c\) er en reel funktion af \(x\), og tegn de niveaukurver der svarer til \(c\in\{−2,−1,0,1,2\}\).

Svar

Niveaukurverne er 5 parabler som er parallelforskudt i forhold til hinanden i \(y\)-aksen retning. Hvad er afstanden mellem dem?

Spørgsmål b#

Vis at punktet \(P=(2,1)\) ligger på niveaukurven svarende til \(c=2\), og find en parameterfremstilling for denne niveaukurve.

Svar

Man kan fx vælge \(\pmb{r}(u)=\left(u,\frac{1}{2}u^2-1\right)\), \(u\in\mathbb{R}\).

Spørgsmål c#

Bestem den til parameterfremstillingen hørende tangentvektor i \(P\), og vis at tangentvektoren er ortogonal på gradienten for \(f\) i \(P\).

Hint

Tangentvektoren får man ved først at differentiere hver af de to koordinatfunktioner i parameterfremstillingen, og dernæst at indsætte parameterværdien for det givne punkt.

Spørgsmål d#

Lav i Python et samlet plot af niveaukurverne og gradientvektorfeltet for \(f\).

Hint

Brug SymPy’s dtuplot.

4: Visualiseringer - tur på et bjerg#

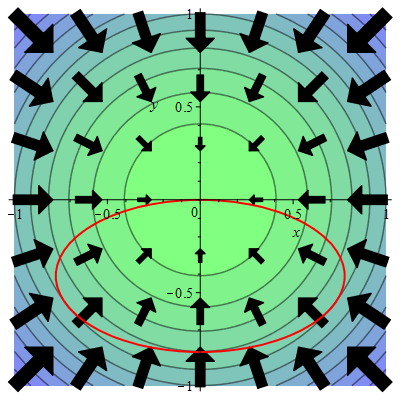
Vi ser på et højdekort for et bjerg, hvor cirklerne er niveaukurver for højdefunktionen. Pilene angiver højdefunktionens gradientvektorfelt. På bjerget findes en elliptisk vandresti som på kortet er rød. Bjerg

Spørgsmål a#

Forestil dig du går en tur langs den røde sti i positiv omløbsretning (mod uret). Find de punkter på stien hvor stigningen er 0 (det går hverken opad eller nedad).

Hint

Der er fire steder.

Svar

På en niveaukurve ændres højden selvfølgelig ikke. Derfor gælder det om at finde de steder på stien hvor stien har fælles tangent med en niveaukurve.

Spørgsmål b#

På hvilke stykker af stien går det opad, og på hvilke nedad?

Spørgsmål c#

Følg nu en af niveaukurverne på tegningen hele vejen rundt og betragt retningen af de gradientvektorer der ligger lige i nærheden. Konklusion?

Spørgsmål d#

Dette bjerg er selvfølgelig ret specielt. Men tag igen vandrestøvlerne på, og giv et intuitivt argument for hvorfor gradientvektorerne altid, på alle bjerge, må være vinkelrette på niveaukurverne?

Svar

Forslag: Hvis vi betragter niveaukurven som en sti vi spadserer ad, er turen stille og rolig. Vi går nemlig hele tiden vandret. Det forekommer naturligt at stigningen må være størst hvis vi brat ændrer retningen med 90 grader opad. Enig?

5: Diskontinuitet af Heaviside’s step function#

Vis at Heaviside’s trin-funktion givet her er diskontinuert i \(x_0=0\).

Hint

En funktion \(f\) er diskontinuert i \(x_0\) hvis vi kan finde et \(\epsilon > 0\) således at intet \(\delta > 0\) kan få \(|x-x_0| < \delta \Rightarrow |f(x)-f(x_0)| < \epsilon\) til at være sand.
Skrevet med kvantorer: \(f\) er diskontinuert i \(x_0\) hvis og kun hvis \(\exists \epsilon >0 \forall \delta >0 \exists x : |x-x_0| < \delta \text{ og } |f(x)-f(x_0)| \ge \epsilon\).

Hint

Vælg \(\epsilon = 1/2\) (den præcise værdi er underordnet så længe den er \(<1\)).

Contents