Uge 4: Spektralsætningen

Uge 4: Spektralsætningen#

Nøglebegreber#

Forberedelse og pensum#

Opgaver – Store Dag#

1: Typer af matricer#

Betragt matricerne:

\[\begin{equation*} A=\begin{bmatrix} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 3 \end{bmatrix}, \quad B=\begin{bmatrix} 1 & 2 & 3 \\ 3 & 1 & 2 \\ 2 & 3 & 1 \end{bmatrix}, \quad C=\begin{bmatrix} 1 & 2+i & 3i \\ 2-i & 1 & 2 \\ -3i & 2 & 1 \end{bmatrix}, \quad D=\begin{bmatrix} i & 2 & 3 \\ 2 & i & 2 \\ 3 & 2 & i \end{bmatrix} \end{equation*}\]

Afgør for hver matrix om den er symmetrisk, hermitisk, og/eller normal. Du må gerne bruge SymPy til at afgøre om matricerne er normale. For nemheds skyld er matricerne skrevet ind her:

A = Matrix.diag(1, 2, 3)
B = Matrix([[1, 2, 3], [3, 1, 2], [2, 3, 1]])
C = Matrix([[1, 2 + I, 3*I], [2 - I, 1, 2], [-3*I, 2, 1]]) 
D = Matrix([[I, 2, 3], [2, I, 2], [3, 2, I]])

Svar

\(A\) er reel og diagonal og derfor automatisk symmetrisk, hermitisk, og normal.

Svar

\(B\) er normal men ikke symmetrisk eller hermitisk.

Svar

\(C\) er hermitisk og derfor også normal, men ikke symmetrisk.

Svar

\(D\) er symmetrisk og normal, men ikke hermitisk (den skal være reel i diagonalen).

2: Hermitisk 2-gange-2 matrix. Håndregning#

Vi betragter den hermitiske matrix \(A\) givet ved:

\[\begin{equation*} A=\begin{bmatrix} 0 & i \\ -i & 0 \end{bmatrix} \end{equation*}\]

Denne opgave går ud på at udregne en spektral dekomposition af \(A\), som vi ved fra Spectral Theorem (the complex case) eksisterer. Vi finder denne dekomposition af \(A\) i tre skridt:

Spørgsmål a#

Find alle egenværdier og tilhørende egenvektorer af \(A\). Kontroller svaret med SymPy A.eigenvects().

Svar

  1. \(\lambda_1 = -1\) med egenvektor \(\pmb{v}_1 = [-i,1]^T\).

  2. \(\lambda_2 = 1\) med egenvektor \(\pmb{v}_2 = [i,1]^T\).

Husk at egenvektorer må ganges med et vilkårlig kompleks tal der ikke er nul. Derfor er fx \(\pmb{v}_1 = [1,i]^T\) (der er ganget med \(i\)) også en egenvektor for \(\lambda_1 = -1\).

Spørgsmål b#

Bestem en ortonormal basis bestående af egenvektorer af \(A\).

Hint

Da \(A\) er hermitisk, ved vi at egenvektorer tilhørende forskellige egenværdier er ortogonale.

Hint

Derfor skal de to egenvektorer blot normaliseres.

Spørgsmål c#

Dette resultat gælder for generelle \(n \times n\) matricer. Vis at \(A = U \Lambda U^*\) hvis og kun hvis \(\Lambda = U^* A U\), når \(U\) er unitær.

Hint

Gang ligningen \(A = U \Lambda U^*\) igennem med \(U^*\) fra venstre og \(U\) fra højre.

Hint

Brug at \(U^* U = I\).

Spørgsmål d#

Opskriv en unitær matrix \(U\) og en diagonalmatrix \(\Lambda\) så \(A = U \Lambda U^*\). Denne formel kaldes en spektral dekomposition af \(A\). Tjek dit resultat med SymPy-kommandoen:

A = Matrix([[0, I], [-I, 0]])
A.diagonalize(normalize = True)

Hint

Find først \(U\). \(U\)’s søjler skal være en ortonormal basis bestående af egenvektorer.

Hint

\(\Lambda\) skal have egenværdierne i diagonalen. Rækkefølgen skal “matche” rækkefølgen på egenvektorerne. Hvis du er I tvivl, så udregn \(\Lambda\) via \(\Lambda= U^* A U\).

3: Symmetrisk 3-gange-3 matrix.#

Givet den reelle og symmetriske matrix

\[\begin{equation*} A=\begin{bmatrix} -2 & 1 & 1 \\ 1 & -2 & -1 \\ 1 & -1 & -2 \end{bmatrix}. \end{equation*}\]

Find en spektral dekomposition af \(A = Q \Lambda Q^T\). Du skal altså angive en reel ortogonal matrix \(Q\) og en diagonalmatrix \(\Lambda\) så

\[\begin{equation*} A = Q \Lambda Q^T \end{equation*}\]

eller, ækvivalent,

\[\begin{equation*} Q^T \, A\, Q=\Lambda \end{equation*}\]

gælder. Som i opgaven før ved vi at den findes fra Spectral Theorem (the real case).

Hint

Find en matrix \( V\), hvis søjler er egenvektorer for \(A\).

Hint

En oplagt mulighed er

\[\begin{equation*}  V=\begin{bmatrix} -1 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \end{bmatrix} \end{equation*}\]

som opfylder, at \( V^{-1}\, A\, V=\Lambda\), med tilhørende diagonalmatrix

\[\begin{equation*} \Lambda=\begin{bmatrix} -4 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & -1 \end{bmatrix}. \end{equation*}\]

Men \(V\) er jo ikke ortogonal?

Hint

\(V\) kan ortogonaliseres ved at benytte Gram-Schmidt på søjlerne.

Hint

Da \(A\) er symmetrisk, er tilhørende egenvektorrum er ortogonale. Så det er kun det to-dimensionale egenvektorrum, du i denne opgave behøver udsættes for Gram-Schmidt. Det éndimensionale egenvektorrum skal blot normaliseres.

Svar

\[\begin{equation*} Q=\begin{bmatrix} -\frac{\sqrt 3}{3} & \frac{\sqrt 2}{2} & \frac{\sqrt 6}{6} \\ \frac{\sqrt 3}{3} & 0 & \frac{\sqrt 6}{3} \\ \frac{\sqrt 3}{3} & \frac{\sqrt 2}{2} & -\frac{\sqrt 6}{6} \end{bmatrix}. \end{equation*}\]

Dette er en blandt flere muligheder. Til dette valg bliver diagonalmatricen \(\Lambda = \mathrm{diag}(-4,-1,-1)\). Hvis du er i tvivl om rækkefølgen af egenværdierne i \(\Lambda\), så kan du udregne \(\Lambda = Q^T A Q\).

4: Spektral dekomposition med SymPy#

Vi betragter følgende matricer givet i SymPy:

A = Matrix([[1, -1, 0, 0], [0, 1, -1, 0], [0, 0, 1, -1], [-1, 0, 0, 1]])
B = Matrix([[1, 2, 3, 4], [4, 1, 2, 3], [3, 4, 1, 2], [2, 3, 4, 1]])
A, B
\[\begin{split}\displaystyle \left( \left[\begin{matrix}1 & -1 & 0 & 0\\0 & 1 & -1 & 0\\0 & 0 & 1 & -1\\-1 & 0 & 0 & 1\end{matrix}\right], \ \left[\begin{matrix}1 & 2 & 3 & 4\\4 & 1 & 2 & 3\\3 & 4 & 1 & 2\\2 & 3 & 4 & 1\end{matrix}\right]\right)\end{split}\]

Det oplyses at begge matricer er reelle, normale matricer. Dette kan tjekkes ved:

A.conjugate() == A, B.conjugate() == B, A*A.T == A.T*A, B*B.T == B.T*B

(True, True, True, True)

Det oplyses endvidere at egenværdierne er hhv:

A.eigenvals(multiple=True), B.eigenvals(multiple=True)
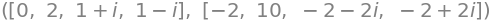
../_images/ec7eb87206e13ae8d94db6d1f94ad93a59b96f56fc73c5f43aebcfc592002b91.png

Spørgsmål a#

Vil nedenstående SymPy-kommandoer give os matricerne der indgår i de spektrale dekompositioner af \(A\) og \(B\)? Kaldet A.diagonalize(normalize = True) returnerer \((V,\Lambda)\) hvor \(A = V \Lambda V^{-1}\) med normaliserede egenvektorer i \(V\) og egenværdierne for \(A\) i diagonalmatricen \(\Lambda\) (jf egenværdiproblemet fra Matematik 1a).

A.diagonalize(normalize = True), B.diagonalize(normalize = True)

Spørgsmål b#

Findes der en unitær matrix der diagonaliserer både \(A\) og \(B\)? Altså, findes der en unitær matrix så \(A = U \Lambda_1 U^*\) og \(B = U \Lambda_2 U^*\), hvor \(\Lambda_1\) er en diagonal matrix med \(A\)’s egenværdier og \(\Lambda_2\) er en diagonal matrix med \(B\)’s egenværdier?

Hint

Hvordan er de to unitære matricer fra forrige spørgsmål relateret?

Svar

Begge unitære matricer fra forrige spørgsmål virker.

Spørgsmål c#

Du har set matricen \(U\) eller \(U^*\) før (eventuelt med søjlerne i en anden rækkefølge). Hvad er det for en matrix?

Svar

\(U\) er den såkaldte Fourier-matrix, se dette eksempel i bogen. I opgaven 4: Unitære matricer betragtede vi netop \(4 \times 4\) Fourier-matricen \(F_4\). Matricerne \(A\) og \(B\) er såkaldte cirkulante matricer der er afbildningsmatricer for (periodisk) foldning (eng: convolution), der bruges i fx convolution neural networks (CNN). Alle sådanne matricer har Fourier matricen som egenvektormatrix \(U\).

5: Diagonalisering og reduktion af kvadratisk form#

Vi betragter funktionen \(q : \mathbb{R}^3 \to \mathbb{R}\) givet ved

\[\begin{equation*} q(x,y,z)=-2x^2-2y^2-2z^2+2xy+2xz-2yz+2x+y+z+5. \end{equation*}\]

Bemærk at \(q\) kan deles op i to led: de “rene” andengradsled \(k(x,y,z)=-2x^2-2y^2-2z^2+2xy+2xz-2yz\) og det andet led: et førstegradspolynomium \(2x+y+z+5\).

Givet den symmetriske matrix

\[\begin{equation*} A=\begin{bmatrix} -2 & 1 & 1 \\ 1 & -2 & -1 \\ 1 & -1 & -2 \end{bmatrix}. \end{equation*}\]

Spørgsmål a#

Angiv en reel, ortogonal matrix \(Q\) og en diagonalmatrix \(\Lambda\), således at

\[\begin{equation*} Q^T \, A\, Q=\Lambda. \end{equation*}\]

Du skal vælge \(Q\) så den har \(\mathrm{det}\,Q=1\). Du må gerne bruge SymPy til denne opgave.

Note

Reelle, ortogonale matricer har altid \(\mathrm{det}\,Q = \pm 1\) (hvorfor mon?), så hvis dit valg \(Q\) har \(\mathrm{det}\,Q = - 1\) kan du blot skifte fortegn på en valgfri søjle eller række. Reelle, ortogonale matricer megd \(\mathrm{det}\,Q = 1\) kaldes sædvanligt orienteret. I \(\mathbb{R}^3\) betyder det blot at den ortonormale basis i \(Q\) er et højredrejet koordinatsystem. Det spiller ikke noget stor rolle for os i denne opgave.

Hint

Med SymPy ser du at \(A\) har \(-4\) som enkelt–egenværdi, men \(-1\) som dobbelt–egenværdi. Derfor skal der gøres lidt arbejde for at finde en ortonormal basis for \(\mathbb{R}^3\) bestående af egenvektorer for \(A\).

Hint

Du kan bruge SymPy’s GramSchmidt på egenvektorerne fra A.eigenvects(). Men måske du kan “gætte”: Vælg en egenvektor fra egenrummet \(E_{-4}\) og en fra \(E_{-1}\). Gæt på en vektor der er vinkelret på begge. Normér dem alle, og du har tre brugbare vektorer til at opstille din \(Q\) med.

Svar

Der er flere muligheder, her har vi valgt:

\(Q=\begin{bmatrix} -\frac{\sqrt 3}{3} & \frac{\sqrt 2}{2} & \frac{\sqrt 6}{6} \\ \frac{\sqrt 3}{3} & 0 & \frac{\sqrt 6}{3} \\ \frac{\sqrt 3}{3} & \frac{\sqrt 2}{2} & -\frac{\sqrt 6}{6} \end{bmatrix}\) og \(\Lambda=\begin{bmatrix} -4 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & -1 \end{bmatrix}.\)

Spørgsmål b#

Bestem forskriften \(k(x,y,z),\) omform den til matrixform, og reducér den.

Hint

Reducere vil sige: Find en (sædvanligt orienteret) ortonormal basis for \(\mathbb{R}^3\) hvori forskriften for \(k\) er uden blandede led.

Hint

Du har sikkert bemærket at den matrix der indgår i matrixform for \(k(x,y,z),\) er identisk med \(A\), så du kan bare bruge den basis med tilhørende diagonalisering, vi lavede ovenfor.

Svar

Hvis vi vælger søjlerne i den fundne \(Q\) som ny ortonormal basis \(\beta\), får vi denne reduktion af \(k:\)

\[\begin{equation*} k(x,y,z) = k(\tilde{x},\tilde{y},\tilde{z}) =-4\tilde{x}^{2}-\tilde{y}^{2}-\tilde{z}^{2}. \end{equation*}\]

Spørgsmål c#

Find en sædvanligt orienteret ortonormal basis for \(\mathbb{R}^3\) hvori forskriften for \(q\) er uden blandede led. Bestem forskriften.

Hint

Vi bruger den ortonormale basis \(\beta\) fundet ovenfor, så er den kvadratiske form klaret. Nu er spørgsmålet så bare hvordan det førstegradspolynomium der indgår i \(q\) tager sig ud i den basis.

Hint

Brug \(Q = {}_e[id]_\beta\) fundet ovenfor som basisskiftematrix, hvor \(e\) angiver standardbasen. Bemærk at \(Q^T = {}_{\beta}[id]_e\). Notation: \({}_{\beta}[id]_e\) er basisskiftematricen fra \(e\)-basis til \(\beta\)-basis og skrives også som \({}_{\beta}M_e\).

Svar

Hvis vi vælger søjlerne i den fundne \(Q\) som ny ortonormal basis \(q\), får \(q\) denne form:

\[\begin{equation*} q(x,y,z) = -4\tilde{x}^{2}-\tilde{y}^{2}-\tilde{z}^{2}+\frac 32\sqrt 2\tilde{y}+\frac 12\sqrt 6\tilde{z}+5. \end{equation*}\]

6: Standardligning for de tre typiske keglesnit#

I de følgende eksempler ser vi på kvadratiske former uden blandede led (da vi jo netop kan slippe af med disse via diagonalisering som i forrige opgave). Her er det muligt at gå skridtet videre og fjerne førstegradsleddene. Denne teknik kaldes kvadratkomplettering. I det følgende skal vi bruge teknikken på vejen mod identifikation af såkaldte keglesnit.

Spørgsmål a#

En ellipse i \((x,y)\)-planen med centrum \((c_1,c_2),\) halvakserne \(a\) og \(b\) og symmetriakserne \(x=c_1\) og \(y=c_2\) har standardligningen

\[\begin{equation*} \frac{(x-c_1)^2}{a^2}+\frac{(y-c_2)^2}{b^2}=1. \end{equation*}\]

En ellipse er givet ved ligningen

\[\begin{equation*} 4x^2+y^2+8x-6y+9=0. \end{equation*}\]

Udfør kvadratkomplettering, sæt ligningen på standardform, og angiv ellipsens centrum, halvakser og symmetriakser.

Hint

Plot den givne ligning med SymPy-kommandoen dtuplot.plot_implicit og tjek dine resultater.

Svar

Centrum \((-1,3).\) Halvakser \(a=1,b=2\). Symmetriakser \(x=-1,y=3.\)

Spørgsmål b#

En hyperbel i \((x,y)\)-planen med centrum \((c_1,c_2),\) halvakserne \(a\) og \(b\) og symmetriakserne \(x=c_1\) og \(y=c_2\) har standardligningen

\[\begin{equation*} \frac{(x-c_1)^2}{a^2}-\frac{(y-c_2)^2}{b^2}=1. \end{equation*}\]

Eller alternativt (hvis den ikke er vandret, men lodret):

\[\begin{equation*} \frac{(y-c_2)^2}{a^2}-\frac{(x-c_1)^2}{b^2}=1. \end{equation*}\]

En hyperbel er givet ved ligningen

\[\begin{equation*} x^2-y^2-4x-4y = 4. \end{equation*}\]

Udfør kvadratkomplettering, sæt ligningen på standardform, og angiv hyperblens centrum, halvakser og symmetriakser.

Hint

Plot den givne ligning med SymPy-kommandoen dtuplot.plot_implicit og tjek dine resultater.

Svar

Centrum \((2,-2).\) Halvakser \(a=2,b=2\). Symmetriakser \(x=2,y=-2.\)

Spørgsmål c#

En parabel i \((x,y)\)-planen med toppunkt \((c_1,c_2)\) og symmetriaksen \(x=c_1\) har standardligningen

\[\begin{equation*} y-c_2=a(x-c1)^2. \end{equation*}\]

Eller alternativt, hvis parablen ikke er lodret men vandret, hvorved symmetriaksen bliver \(y=c_2\):

\[\begin{equation*} x-c_1=a(y-c2)^2. \end{equation*}\]

En parabel er givet ved ligningen

\[\begin{equation*} 2x^2+12x-y+17=0. \end{equation*}\]

Udfør kvadratkomplettering, sæt ligningen på standardform, og angiv parablens toppunkt og symmetriakse.

Hint

Plot den givne ligning med SymPy-kommandoen dtuplot.plot_implicit og tjek dine resultater.

Svar

Toppunkt \((-3,-1).\) Symmetriakse: \(x=-3.\)

7: Den partielle afledte vokser/aftager mest i gradient-retningen#

Denne opgave er taget fra bogen, og formålet er at argumentere for, hvorfor man i gradient-metoden går i gradientvektorens retning.

Lad \(f: \mathbb{R}^{n} \to \mathbb{R}\) være en funktion, for hvilken alle retningsafledte eksisterer i \(\pmb{x} \in \mathbb{R}^{n}\). Antag at \(\nabla f(\pmb{x})\) ikke er nul-vektoren.

Spørgsmål a#

Vis at \(\pmb{u} := \nabla f(\pmb{x}) / \Vert \nabla f(\pmb{x}) \Vert\) er en enhedsvektor.

Spørgsmål b#

Vis at skalaren \(|\nabla_{\pmb{v}}f(\pmb{x})|\) bliver størst mulig, når \(\pmb{v} = \pm \pmb{u}\).

Hint

Husk at \(\nabla_{\pmb{v}}f(\pmb{x})) = \langle \pmb{v}, \nabla f (\pmb{x}) \rangle\). Hvad får du hvis du indsætter \(\pmb{u} = \nabla f(\pmb{x}) / \Vert \nabla f(\pmb{x}) \Vert\)?

Hint

Brug Cauchy/Schwarz’s ulighed til at argumentere at \(|\nabla_{\pmb{v}}f(\pmb{x})|\) ikke kan blive større.

Svar

Fra Cauchy-Schwarz’s uligheden ser vi først at \(| \nabla_{\pmb{v}}f(\pmb{x})) |= | \langle \pmb{v}, \nabla f (\pmb{x}) \rangle | \le \Vert \pmb{v} \Vert \, \Vert \nabla f (\pmb{x})\Vert = \Vert \nabla f (\pmb{x})\Vert\) for alle enhedsvektorer \(\pmb{v}\). Med \(\pmb{v} = \nabla f(\pmb{x}) / \Vert \nabla f(\pmb{x}) \Vert\) fås

\[\begin{equation*} \nabla_{\pmb{v}}f(\pmb{x}) = \langle \nabla f(\pmb{x}) / \Vert \nabla f(\pmb{x}) \Vert, \nabla f (\pmb{x}) \rangle = \langle \nabla f(\pmb{x}) , \nabla f (\pmb{x}) \rangle / \Vert \nabla f(\pmb{x}) \Vert = \Vert \nabla f(\pmb{x}) \Vert^2 / \Vert \nabla f(\pmb{x}) \Vert = \Vert \nabla f(\pmb{x}) \Vert, \end{equation*}\]

hvilket er lig med den maksimale værdi.

8: Reel symmetrisk 2-gange-2 matrix.#

Vi betragter en vilkårlig reel, symmetrisk \(2 \times 2\) matrix. En sådan matrix kan skrives:

\[\begin{equation*} A=\begin{bmatrix} a & c \\ c & b \end{bmatrix} \end{equation*}\]

hvor \(a,b\) og \(c\) er reelle tal.

Spørgsmål a#

Vis at \(A\)’s egenværdier er reelle.

Hint

Er \(A\) hermitisk? Der er et resultat i lærebogens afsnit 2.8 man kan bruge direkte.

Hint

Man kan alternativt kigge på fortegnet af diskriminanten for det karakteristiske polynomium, og derefter konkludere at der kun er reelle rødder.

Svar

Det følger direkte af Lemma 2.8.1, da \(A\) er hermitisk.

Argumentet via det karakteristiske polynomium er som følger: Der gælder

\[\begin{equation*} \det (A-\lambda I)=0\Rightarrow\lambda^2+(-a-b)\lambda+ab-c^2=0. \end{equation*}\]

Da diskriminanden til denne ligning er

\[\begin{equation*} d=(a-b)^2+4c^2\geq 0, \end{equation*}\]

vil \(A\) have to reelle rødder (regnet med multiplicitet). Bemærk, at det omvendte ikke gælder: To reelle egenværdier kan også fremkomme af en ikke-symmetrisk matrix.

Spørgsmål b#

Vis at hvis \(A\) ikke er en diagonalmatrix, så har den to forskellige (reelle) egenværdier.

Hint

Kig igen på diskriminanten for det karakteristiske polynomium.

Svar

Diskriminanten er 0, netop når \(c=0\) og \(a=b\).

Temaøvelse – Lille Dag#

Der er tema-øvelse Tema 2: Data-matricer og Dimensionsreduktion

Contents