Uge 6: Ekstrema og Optimering

Demo af Christian Mikkelstrup, Hans Henrik Hermansen, Jakob Lemvig, Karl Johan Måstrup Kristensen og Magnus Troen

from sympy import *
from dtumathtools import *
init_printing()

Når man skal til at undersøge ekstrema af en funktion \(f:\Omega \to \mathbb{R}\) er der i princippet 3 områder, som skal undersøges. I Theorem 5.2.2 beskrives de ved

1. \(\boldsymbol{x}_0 \in \partial \Omega \cap \Omega\) (altså min og/eller max kan være et punkt på randen af definitionsmængden \(\Omega\))

2. \(\boldsymbol{x}_0\) er et punkt hvor \(f\) ikke differentiabel (kladet undtagelsespunkt i det følgende)

3. \(\boldsymbol{x}_0\) er et punkt hvor \(f\) er differentiabel og \(\nabla f(\boldsymbol{x}_0) = 0\) (kaldet et stationært punkt)

Lokale ekstrema, eksempel 1

Vi vil forsøge at finde alle ekstremumspunkter for funktionen \(f: \mathbb{R}^2 \to \mathbb{R}\) givet ved:

\[\begin{equation*} f(x,y) = x^3 - 3x^2 + y^3 - 3y^2. \end{equation*}\]

Vi bemærker at \(f\) er defineret og differentiabel på alle punkter i \(\mathbb{R}^2\). Der er alstå ingen rand- eller undtagelsespunkter, vi bør undersøge.

Derfor kan vi nøjes med at undersøge de stationære punkter, der er givet ved løsningen til ligningerne:

x,y = symbols("x y", real=True)
f =  x**3 - 3 * x**2 + y**3 - 3 * y**2
lign1 = Eq(f.diff(x),0)
lign2 = Eq(f.diff(y),0)
display(lign1,lign2)

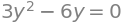
Disse ligninger er ikke-lineære, men løses alligevel let, enten i hånden eller i SymPy:

sols = nonlinsolve([lign1, lign2], [x,y])
sols

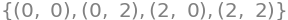
Nu har vi vores stationære punkter. Nu kan vi finde de partielt afledede af 2. orden og opstille Hessematricen.

H = dtutools.hessian(f)
H

\[\begin{split}\displaystyle \left[\begin{matrix}6 x - 6 & 0\\0 & 6 y - 6\end{matrix}\right]\end{split}\]

Derefter indsættes de stationære punkter, og egenværdierne for \(\boldsymbol{H}_f\) undersøges, hvilket er nemt, da \(H\) allerede er diagonaliseret, og egenværdierne derfor direkte kan aflæses af matricen.

[{(x0, y0): H.subs([(x,x0),(y,y0)])} for (x0,y0) in sols]

\[\begin{split}\displaystyle \left[ \left\{ \left( 0, \ 0\right) : \left[\begin{matrix}-6 & 0\\0 & -6\end{matrix}\right]\right\}, \ \left\{ \left( 0, \ 2\right) : \left[\begin{matrix}-6 & 0\\0 & 6\end{matrix}\right]\right\}, \ \left\{ \left( 2, \ 0\right) : \left[\begin{matrix}6 & 0\\0 & -6\end{matrix}\right]\right\}, \ \left\{ \left( 2, \ 2\right) : \left[\begin{matrix}6 & 0\\0 & 6\end{matrix}\right]\right\}\right]\end{split}\]

Theorem 5.2.4 fortæller os nu at \(f\) i punktet:

• \((0,0)\) antager (attains i eNoterne) et egentligt (lokalt) maksimum, da begge egenværdier aflæses til at være negative

• \((2,2)\) antager et egentligt (lokalt) minimum, da begge egenværdier aflæses til begge at være positive

• \((0,2)\) har saddelpunkt, da egenværdierne har modsat fortegn

• \((2,0)\) har saddelpunkt efter samme argument som \((0,2)\)

Et saddelpunkt er et stationært punkt der ikke er et lokalt ekstremumspunkt. Bemærk at der er tale om lokale ekstremumsværdier. Funktionen har ingen maksimums- eller minimumsværdi, da man kan vise at \(\mathrm{im}(f)=]-\infty,\infty[\).

# Show points
list_of_stationary_points = [Matrix([x0,y0,f.subs([(x,x0),(y,y0)])]) for (x0,y0) in sols]
points = dtuplot.scatter(list_of_stationary_points, show=False, rendering_kw={"s" : 100,"color":"red"})

# Show the surface f with the stationary points
pf = dtuplot.plot3d(f,(x,-0.8,2.8),(y,-0.8,2.8),use_cm=True, colorbar=False,show=False,wireframe=True,rendering_kw={"alpha":0.6})
pf.camera = {"azim" : -50, "elev" : 30}
pf.extend(points)
pf.show()

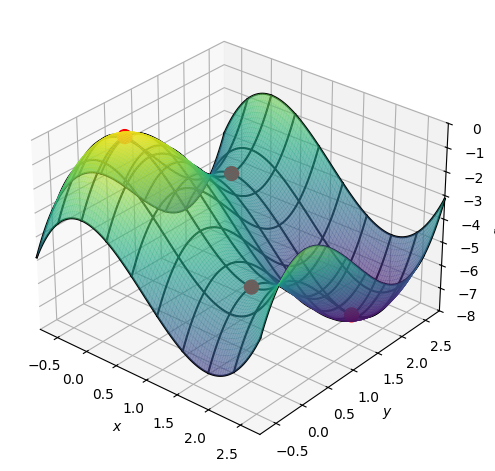
Lokale ekstrema, eksempel 2

Vi betragter nu funktionen \(f:\mathbb{R}^2 \to \mathbb{R}\) givet ved

\[\begin{equation*} f(x,y) = x^4 + 4x^2y^2 + y^4 -4x^3 - 4y^3 + 2 \end{equation*}\]

Definitionsmængden er hele \(\mathbb{R}^2\), altså er der ingen rand- eller undtagelsespunkter vi bør undersøge. Derfor nøjes vi med at undersøge de stationære punkter.

x,y = symbols('x y', real=True)

f = x ** 4 + 4 * x**2 * y ** 2 + y ** 4 - 4 * x ** 3 - 4 * y ** 3 + 2
lign1 = Eq(f.diff(x),0)
lign2 = Eq(f.diff(y),0)
lign1,lign2,f

sols = nonlinsolve([lign1,lign2], [x, y])
sols

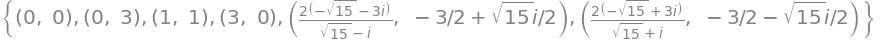
[(N(xsol),N(ysol)) for (xsol,ysol) in sols]

\(\verb|nonlinsolve()|\) tager ikke højde for hvordan vi har defineret vores variable, så selvom vi har prøvet at definere \(x,y\) med \(\verb|real=True|\), skal man her selv bruge hovedet. Vi kan her se, at der findes fire (reelle) stationære punkter. Nemlig:

stat_punkter = list(sols)[:-2] # Remove the last two elements (complex solutions) with list-slicing
stat_punkter

Lad os finde Hessematricen for at kunne undersøge punkterne.

H = dtutools.hessian(f)
H

\[\begin{split}\displaystyle \left[\begin{matrix}12 x^{2} - 24 x + 8 y^{2} & 16 x y\\16 x y & 8 x^{2} + 12 y^{2} - 24 y\end{matrix}\right]\end{split}\]

Vi indsætter de stationære punkter og da \(\boldsymbol{H}_f\) ikke er diagonaliseret på forhånd som i sidste eksempel, må vi bede SymPy om egenværdierne

Hesse_matricer = [H.subs([(x,x0),(y,y0)]) for x0,y0 in stat_punkter]
Eig_Hesse_matricer = [h.eigenvals() for h in Hesse_matricer]

display(*zip(stat_punkter,Eig_Hesse_matricer))

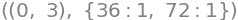
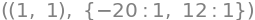
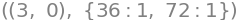
Heraf kan vi aflæse at \(f\) har egenligt minimum i både \((0,3)\) og \((3,0)\). Vi kan se at \((1,1)\) er saddelpunkt og ikke et ekstremum, da der både er positiv og negativ egenværdi.

Da \(\boldsymbol{H}_f((0,0))\) har mindst en egenværdi som er er nul, er vi nødt til at lave en særundersøgelse af punktet \((0,0)\). Lad os prøve at se hvordan \(f\) opfører sig på linjen \(y=x\).

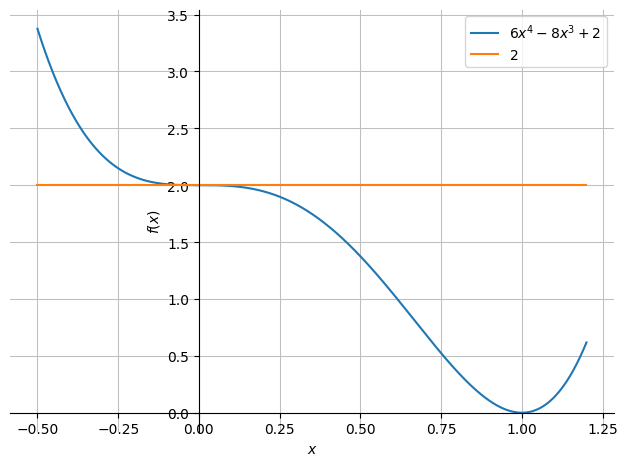
dtuplot.plot(f.subs(y,x),2,(x,-0.5,1.2),axis_center="auto")

<spb.backends.matplotlib.matplotlib.MatplotlibBackend at 0x7f1ff1cc5f40>

Allerede her er det meget tydeligt, at \((0,0)\) hverken er et minimums- eller maksimumspunkt. Vi kan undersøge dette lidt nærmere:

tmp = f.subs(y,x) - f.subs([(x,0),(y,0)])
display(tmp, tmp.factor())

Heraf kan vi se

\(f(x,x) - f(0,0) > 0\) når \(x < 0\) og \(f(x,x) - f(0,0) < 0\), når \(0 < x < \frac{4}{3}\)

Da \(f(x,x)\) antager værdier der både er større og mindre end \(f(0,0)\) for \((x,x)\) virkårligt tæt på \((0,0)\), kan \(f\) ikke have ekstremum i \((0,0)\).

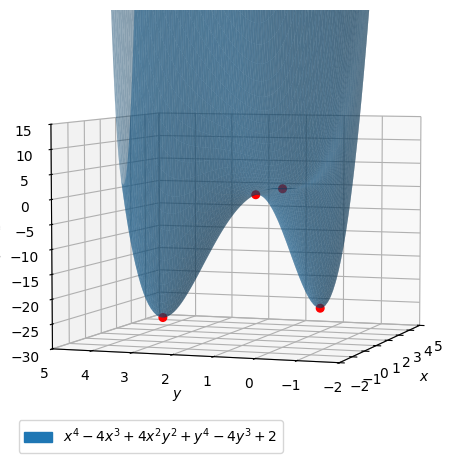
Lad os se grafen for \(f\) sammen med de stationære punkter.

list_of_stationary_points = [Matrix([x0,y0,f.subs([(x,x0),(y,y0)])]) for (x0,y0) in stat_punkter]
points = dtuplot.scatter(list_of_stationary_points, show=False, rendering_kw={"color":"red", "s" : 30})

pf = dtuplot.plot3d(f,(x,-2, 5),(y,-2, 4),xlim=(-2,5),ylim=(-2,5),zlim=(-30,15), show=False, rendering_kw={"alpha":0.5})
pf.camera = {"azim" : -161, "elev" : 5}
(pf + points).show()

Globale ekstrema på begrænset og afsluttet mængde, eksempel 1

Vi betragter nu funktionen \(f:\Omega \to \mathbb{R}\) med forskriften.

\[\begin{equation*} f(x,y) = 3 + x - x ^ 2 - y ^ 2 \end{equation*}\]

Igen er \(f\) veldefineret på hele \(\mathbb{R}^2\), men denne gang er definitionsmængden begrænset ved

\[\begin{equation*} \Omega := \Bigl\{(x,y) \in [0,2]\times[-1,1]\quad |\quad y \leq 1-x\Bigr\}, \end{equation*}\]

altså den mængde der indesluttes af linjerne \(y = -1\), \(y = 1-x\) og \(x=0\).

M = dtuplot.plot_implicit(Eq(x,0),Eq(y,1-x),Eq(y,-1), (1-x >= y) & (y >= -1) & (x >= 0),(x,-0.1,2.1),(y,-1.1,1.1),show=False)
M.legend = False
M.show()

The provided expression contains Boolean functions. In order to plot the expression, the algorithm automatically switched to an adaptive sampling.

Vi bemærker at \(f\) er differentiabel over hele \(\Omega\), så der er ingen undtagelsespunkter, vi skal tage hensyn til. Derfor er den også kontinuert på hele \(\Omega\). Da \(\Omega\) er afsluttet og begrænset, har \(f\) derfor et globalt minimum og maksimum på \(\Omega\). De to værdier må enten antages i stationære punter eller på randen.

Da \(\Omega\) er en sammenhængende mængde, er værdimængden for \(f(\Omega) = [m;M]\), hvor \(m\) er det globale minimum, og \(M\) er et globale maksimum.

Lad os først kigge på \(f\)’s niveaukurver

f = 3 + x - x ** 2 - y ** 2
niveau = dtuplot.plot_contour(f,(x,-0.1,2.1),(y,-1.1,1.1),show=False)
niveau.extend(dtuplot.plot_implicit(Eq(x,0),Eq(y,1-x),Eq(y,-1),(x,-0.1,2.1),(y,-1.1,1.1),show=False))
niveau.show()

Lad os nu bestemme de stationære punkter.

lign1 = Eq(f.diff(x),0)
lign2 = Eq(f.diff(y),0)
sols = nonlinsolve([lign1,lign2], [x,y])
sols

Vi kan se at punkter ligger i \(\Omega\), og er derfor et relevant stationært punkt. Lad os plotte restriktionen af \(f\) til hver af de tre randlinjer. Derefter findes de stationære punkter for disse tre randlinjer.

dtuplot.plot(f.subs(y, -1),(x,0,2), title="Randlinjen f(x, -1)")

<spb.backends.matplotlib.matplotlib.MatplotlibBackend at 0x7f1ff1dd87c0>

dtuplot.plot(f.subs(y, 1-x),(x,0,2), title="Randlinjen f(x, 1-x)")

<spb.backends.matplotlib.matplotlib.MatplotlibBackend at 0x7f2011a3ea60>

dtuplot.plot(f.subs(x,0), (y,-1,1), ylim = (0,3),aspect="equal", title="Randlinjen f(0, y)")

<spb.backends.matplotlib.matplotlib.MatplotlibBackend at 0x7f1ff272dc70>

stat_punkter = set(sols)

lodret = solve(f.subs(x,0).diff(y))
vandret = solve(f.subs(y,-1).diff(x))
skrå = solve(f.subs(y,1-x).diff(x))

stat_punkter.update(set([(0,y0) for y0 in lodret]))
stat_punkter.update(set([(x0,-1) for x0 in vandret]))
stat_punkter.update(set([(x0,1-x0) for x0 in skrå]))
stat_punkter

Nu skal vi blot finde maksimum og minimum mellem de fundne stationære punkter og randlinjernes endepunkter, så \((0,1)\), \((0,-1)\) og \((2,-1)\)

undersøgelses_punkter = list(stat_punkter) + [(0,1),(0,-1),(2,-1)]
f_værdier = [f.subs([(x,x0),(y,y0)]) for x0,y0 in undersøgelses_punkter]

minimum = min(f_værdier)
maximum = max(f_værdier)
f_værdier, minimum, undersøgelses_punkter[f_værdier.index(minimum)], maximum, undersøgelses_punkter[f_værdier.index(maximum)]

Nu har vi endelig:

Globalt minimum: \(0\) i punktet \((2,-1)\)
Globalt maximum: \(\frac{13}{4}\) i punktet \((\frac{1}{2},0)\)
Værdimængde: \([0,\frac{13}{4}]\)

Lad os plotte det hele samlet

u = symbols("u")
pf = dtuplot.plot3d(f,(x,0,2),(y,-1,1),show=False,rendering_kw={"alpha":0.7})
punkter = dtuplot.scatter([Matrix([2,-1,0]),Matrix([1/2,0,13/4])],show=False,rendering_kw={"color":"red","s":20})
l1 = dtuplot.plot3d_parametric_line(u,-1,f.subs({x:u,y:-1}),(u,0,2),use_cm=False,show=False,rendering_kw={"color":"red","linewidth":2})
l2 = dtuplot.plot3d_parametric_line(0,u,f.subs({x:0,y:u}),(u,-1,1),use_cm=False,show=False,rendering_kw={"color":"red","linewidth":2})
l3 = dtuplot.plot3d_parametric_line(u,1-u,f.subs({x:u,y:1-u}),(u,0,2),use_cm=False,show=False,rendering_kw={"color":"red","linewidth":2})
combined = (pf + punkter + l1 + l2 + l3)
combined.camera = {"azim" : 148, "elev" : 40}
combined.legend = False

combined.show()