Projektappetizere

• Miljø, BioTek, TekBio, BærEnergi, Design, KunsInt & DataSci kan danne grupper sammen og skal vælge mellem

  1. Fra Valle til Tagatose

  2. Udsivning fra affaldsdeponier

  3. Selvkørende biler

• MedTek, Elektro kan danne grupper sammen og skal vælge Vektoranalyse i elektromagnetismen

• Byg Tek, Byg Des, MatTek, Software, Cyber, CompTek, KemiTek, Produktion kan danne grupper sammen og skal vælge mellem

  1. Selvkørende biler

  2. Optiske bølgeledere

  3. PageRank af hjemmesider (ikke MatTek)

  4. Optimal opsætning af solpaneler

• Fysik, Geo Fys kan danne grupper sammen og skal vælge Vektoranalyse i elektromagnetismen

• BSc Teknologi skal vælge projekt om Tomografi og CT-skannere

Fra Valle til Tagatose

Denne opgave går ud på at studere nogle vigtige forhold i forbindelse med anvendelse af enzymer i produktionsprocesser. Som model anvendes fjernelse af laktose fra valle, idet laktosen hydrolyseres til glukose og galaktose, der videre kan omdannes tagatose.

Projektet er opdelt i 3 faser:

• Fase 1 indfører de grundlæggende reaktionskinetiske elementer og begreber i enzymkatalyserede processer. Herunder initialhastigheder, kompetetiv inhibering og det integrerede procesforløb.

• Fase 2 tager udgangspunkt i reaktionernes temperaturfølsomhed, herunder begrænsninger i reak- tionstid (pga. evt. vækst af mikroorganismer) og denaturering af enzymer.

• Fase 3 handler om optimering.

Projektet handler om emner som løsning af differentialligninger og bestemmelse af minimum for en funktion af flere variable med henblik på optimering af en proces.

Problemstillingerne behandles med hjælp af Sympy. Der benyttes primært Sympy kommandoer, der tidligere har været benyttet i Matematik 1.

Udsivning fra affaldsdeponier

Forurening er et globalt - og et lokalt problem. Forurening af omkringliggende jordområder transporteres til vandløb bl.a. via grundvandsstrømning. Denne forurening kan f.eks. bestå i pesticider, der sprøjtes på marker eller i sjældnere tilfælde af ikke-genanvendeligt a↵ald, der er placeret i såkaldte deponier. Forureningen kan udgøre en trussel mod de planter og dyr, der lever i vandet. Derfor er det vigtigt at kunne bestemme, hvor lang tid det tager for forureningen af bevæge sig ned til vandet?

Formålet med opgaven er at analysere en simpel model for hvordan forurening transporteres ved hjælp af grundvandsstrømning. Fysisk set er en sådan transport beskrevet ved Darcy’s lov:

\[ Q = -K_s A \frac{\partial h}{\partial x} \]

Darcy’s lov svarer til Ohms lov for elektriske kredsløb.

Matematisk set handler projektet om emner som løsning af lineære og ikke-lineære differentialligninger for \(h(x)\) via numeriske og eksakte metoder (f.eks. via diagonalisering). Derudover omhandler den bestemmelse af minimum for en funktion af flere variable med henblik på tilpasning af modellen til måledata. Opgaven skulle således være tilgængelig for alle med en interesse i simple matematiske modeller.

Selvkørende biler og konvojdynamik

Trafikflow og bilers adfærd er vigtige faktorer for moderne transport. I takt med udviklingen af selvkørende biler opstår nye udfordringer: Hvordan sikrer vi en stabil og sikker kørsel i en konvoj? Hvad sker der, når en bil bremser pludseligt, og hvordan forplanter denne ændring sig gennem rækken af køretøjer?

Formålet med dette projekt er at analysere en simpel matematisk model for selvkørende biler i en konvoj. Hver bil justerer sin acceleration baseret på afstanden til bilen foran og forskellen i hastighed. Modellen beskrives ved en differentialligning:

\[ a(t) = b(v^+(t) - v(t)) + c(x(t) - x^*(t)) \]

hvor \(v(t)\) er bilens hastighed, \(x(t)\) er afstanden til den forankørende bil, og \(x^*(t) = Tv^+(t)\) er den ønskede afstand.

Matematisk set omhandler projektet analyse og løsning af lineære differentialligninger, stabilitetsundersøgelser samt numeriske simuleringer af bilernes bevægelse. Opgaven bruger kun i lille grad Python.

Optiske bølgelederes modes, ulineariteter og kvanteoptik

Optiske fibre udgør rygraden af den moderne internettrafik, som i dag håndterer adskillige terabit per sekund (\(10^{12}\) bit/s). De konstante krav til at øge kapaciteten udfordrer fibernettet og leder til nye måder at transportere mere data. En metode, der har stor interesse, er at bruge lysets rumlige fordeling i fiberen til at indkode data.

I en fiber kan lyset kun antage visse rumlige fordelinger, såkaldte modes. Ved at kommunikere data separat i hver mode kan man potentielt mangedoble datakapaciteten i optiske fibre. Disse modes har dog også mange andre anvendelser – for eksempel i ikke-lineære processer og kvanteoptik.

I denne opgave skal I arbejde med de grundlæggende ligninger, der styrer, hvordan lys opfører sig. Efter at have udledt bølgeligningen for det elektromagnetiske felt, skal I finde løsninger for en optisk fiber. Dette leder til optiske modes, dvs. diskrete fordelinger af lyset i fiberens transverse plan.

Vi vil derefter undersøge, hvordan de unikke egenskaber af de forskellige modes kan anvendes i en såkaldt ikke-lineær proces, hvor kun enkelte fotoner bliver skabt. Især vil vi undersøge, hvordan de forskellige fiber-modes kan bruges til at skræddersy kvantetilstanden af disse fotoner. De kvantemekaniske fotoner kan herefter anvendes i eksempelvis en optisk kvantecomputer.

Hvis alle dele af opgaven gennemføres, vil I kunne designe jeres egen optiske fiber: Hvor tæt kan I komme på den ideelle enkeltfotonkilde?

Projektet inkluderer bl.a. følgende matematiske emner:

• Komplekse tal

• Vektorfelter og vektorcalculus

• Funktioner af flere variable

• Matricer og matrixregning

• Lineære differentialligninger

Derudover vil I stifte bekendtskab med ny matematik såsom:

• Besselfunktioner

• Kontinuerte egenværdiproblemer

• Singular value decompositions

Dette projekt giver jer mulighed for at anvende teoretiske matematiske metoder i en højteknologisk og fremadskuende kontekst!

PageRank – Matematikken bag Googles søgealgoritme

Hvordan bestemmes rækkefølgen af søgeresultater på nettet? PageRank-algoritmen, udviklet af Google, bruger matematiske modeller til at rangere hjemmesider baseret på deres linkstruktur.

I projektet vil du undersøge, hvordan hjemmesider kan repræsenteres som rettede grafer, hvordan linkmatrixen opbygges, og hvordan PageRank beregnes ved hjælp af Markov-kæder og iterative metoder. Undervejs vil du arbejde med sandsynlighedsvektorer, matrixmultiplikation, egenværdier, spektralsætningen, tidsdiskrete dynamikker og Python-implementeringer af algoritmen.

Projektet kombinerer matematik, datalogi og anvendelser i netværksanalyse – en perfekt mulighed for at se teori i praksis! Bemærk: Projektet bruger i høj grad Python.

Optimal opsætning af solpaneler

En husejer nær DTU ønsker at opsætte solpaneler på sit parcelhus med fladt tag. Han tænker han skal vende dem mod syd, men er i tvivl om hvilken vinkel panelet bør danne med taget.

I dette projekt skal I finde den optimale vinkel for husejerens solpaneler. Projektets mål er at udvikle en model og et Python-program der for angivet placering på jorden (længde- og breddegrad) kan udregne den optimale vinkel for opsætning af solpaneler under en række simplificerende antagelser. Til simulering skal bruges data fra kalenderåret 2025. I starter med at modellere solens bevægelse på himlen ved hjælp af Python-pakken pvlib. I skal herefter opstille en model for solpanelets energioptag, der ikke tager højde for skyer og atmosfære. Solen modelleres som en vektorfelt af parallelle vektorer. For at udregne energioptaget skal I kunne integrere vektorfeltets flux gennem solpanelfladen. Solpanelets placering optimeres med hensyn til:

• at maksimere energiproduktion

• at minimere husejerens samlede udgifter til el

I skal efterfølgende prøve at modificere jeres model til at tage højde for fx jordens atmosfære, skyer og skygge.

Bemærk: Projektet bruger i høj grad Python.

Vektoranalyse i elektromagnetismen

Gauss’ og Stokes’ sætninger er centrale værktøjer i fysik og ingeniørvidenskab. De bruges blandt andet i elektromagnetismen til at beskrive, hvordan elektriske og magnetiske felter opfører sig.

I projektet vil du undersøge de matematiske principper bag disse sætninger og anvende dem til at analysere Maxwell’s ligninger. Undervejs vil du arbejde med vektorfelter, divergens, rotation og integraler samt løse problemer relateret til elektromagnetiske felter. Projektet kombinerer teori med praktiske beregninger og har anvendelser inden for fx strømning i væsker og design af elektriske kredsløb.

I projektet indgår matematik som:

• Vektorfelter og vektoroperatoren nabla

• Divergens, rotation, flux, og gradient

• Lineintegraler og fladeintegraler

• Koordinattransformationer

• Anvendelse af lineær algebra til elektromagnetiske problemer

Hvordan hænger matematik og elektromagnetisme sammen? Dette projekt giver dig svaret.

Tomografi og CT skannere

Hvordan vi med matematik kan se det skjulte

På hospitaler laver man rutinemæssigt CT-skanninger. Resultaterne er skanningsbilleder, som er særdeles nyttige til fx at diagnosticere kræft eller analysere komplicerede brud. CT er en forkortelse for Computerised Tomography, og det handler grundlæggende om at lave billeder ved brug af røntgenstråler.

En CT-skanner har en røntgenkilde, som skyder stråler gennem patienten langs rette linjer. En detektor måler så på modsatte side af patienten, hvordan strålernes intensitet er aftaget undervejs. Ved at løse et inverst problem kan man lave præcise billeder af kroppens indre strukturer. Dette involverer avanceret teknologi, fysik og dyb og spændende matematik. Præcis samme matematik og teknologi bruges til at skanne vindmøllevinger, gasrør under havets overflade og kornstrukturer i metaller.

I dette projekt skal du stifte bekendtskab med matematikken og fysikken bag CT.
Du vil undersøge de målinger, der kommer ud af en sådan skanning, og hvordan man rekonstruerer et billede ud fra målingerne.

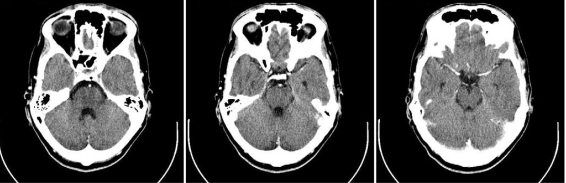
Projektet indeholder både matematisk teori og computerberegninger.

Første del: Matematisk teori. Du vil arbejde teoretisk med kernestof fra Matematik 1, herunder:

• Funktioner af flere variable

• Koordinattransformationer

• Linjeintegraler

• Førsteordens differentialligninger med variable koefficienter

I krydsfeltet mellem disse emner støder vi på Inverse Problemer og Radon-transformationen.

Anden del: Numerisk rekonstruktion. Du vil undersøge, hvordan man med lineær algebra og matrixberegninger på en computer kan løse CT-problemet og rekonstruere skarpe billeder.

Matematik, teknologi og virkelige anvendelser. Dette projekt giver en dybere forståelse af, hvordan matematik og fysik bruges til at løse praktiske problemer i både medicin og ingeniørvidenskab. Har du nogensinde tænkt over, hvordan vi kan se det skjulte? Dette projekt vil give dig svaret!