Uge 2: Differentiabilitet

Demo af Christian Mikkelstrup, Hans Henrik Hermansen, Karl Johan Måstrup Kristensen og Magnus Troen

from sympy import *
from dtumathtools import *
init_printing()

Når det kommer til Python/CAS og differentiabilitet, har vi samme problem som med kontinuitet. Python/CAS egner sig ikke særlig godt til at bevise differentiabilitet, men det kan være et stærkt værktøj når differentiabilitet først er bevist. I denne demo vil vi se på nogle af de mulige anvendelser.

Vektorfunktioner

En vektorfunktion af flere variable er defineret i def 1.3.1 og kan som bekendt skrives op ved

\[\begin{split}\boldsymbol f(\boldsymbol x) = \begin{bmatrix} f_1(\boldsymbol x) \\ \vdots \\ f_k(\boldsymbol x) \end{bmatrix}\end{split}\]

Vi kender allerede eksempler på vektor funktioner af flere variable fra linear algebra, nemlig linære afbildninger fra \(\mathbb R^n\) til \(\mathbb R^k\). Som med en vilkårlig \(k \times n\) matrix \(A\) og vektor \(\boldsymbol x \in \mathbb R^n\) ville have formen

\[\begin{split}\boldsymbol f(\boldsymbol x) = A\boldsymbol x = \begin{bmatrix} f_1(\boldsymbol x) \\ \vdots \\ f_k(\boldsymbol x) \end{bmatrix}.\end{split}\]

Her er funktionerne \(f_1, f_2, \ldots, f_k\) altså bestemt af matrix-vektor multiplikationen I lærte i Mat1a. Forskellen fra de generelle vektorfunktioner af flere variable er nu at koordinatfunktionerne \(f_1, f_2, \ldots, f_k\) ikke er begrænset af krav om linearitet som \(f_i(x_1,x_2,x_3) = c_1x_1 + c_2x_2 + c_3x_3\). En koordinatfunktion \(f_i\) kunne for eksempel have forskriften \(f_i(x_1,x_2,x_3) = x_1 \sin(x_2) + x_3^2\).

I SymPy kan man bruge Matrix-objektet eller funktioner til at konstruere disse vektor funktioner, meget gennemgangen af funktioner fra uge 1-demoen:

# Example of a vector function using the Matrix class
x1, x2, x3 = symbols('x1:4')

f_expr = Matrix([
    x1 * sin(x2) + x3**2,
    x1*x2*x3,
    x1**2 + 4*x2 * x3
])
f_expr

\[\begin{split}\displaystyle \left[\begin{matrix}x_{1} \sin{\left(x_{2} \right)} + x_{3}^{2}\\x_{1} x_{2} x_{3}\\x_{1}^{2} + 4 x_{2} x_{3}\end{matrix}\right]\end{split}\]

Hvor input kan gives ved brug af \(\verb|.subs()|\)

f_expr.subs({x1: 1, x2: 2, x3: 3})

\[\begin{split}\displaystyle \left[\begin{matrix}\sin{\left(2 \right)} + 9\\6\\25\end{matrix}\right]\end{split}\]

Hvis man er mere til funktioner kan man gøre således

def f(x1, x2, x3):
    return Matrix([
        x1 * sin(x2) + x3**2,
        x1*x2*x3,
        x1**2 + 4 * x2 * x3
    ])

f(x1,x2,x3)

\[\begin{split}\displaystyle \left[\begin{matrix}x_{1} \sin{\left(x_{2} \right)} + x_{3}^{2}\\x_{1} x_{2} x_{3}\\x_{1}^{2} + 4 x_{2} x_{3}\end{matrix}\right]\end{split}\]

f(1,2,3)

\[\begin{split}\displaystyle \left[\begin{matrix}\sin{\left(2 \right)} + 9\\6\\25\end{matrix}\right]\end{split}\]

Begge fremgangsmåder opnår det samme, hvad man så personligt ønsker at bruge er en smagssag.

Gradientvektor

Et andet godt eksempel på en vektorfunktion findes i gradientvektoren af en skalar-funktion \(f: \mathbb{R}^n \to \mathbb{R}\) introduceret i sidste uge:

\[\nabla f(\boldsymbol x):=\left(\frac{\partial f}{\partial x_1}(\boldsymbol x),\frac{\partial f}{\partial x_2}(\boldsymbol x),\ldots, \frac{\partial f}{\partial x_n}(\boldsymbol x)\right).\]

Dette kan ses som en afbildning \(\nabla f: \mathbb{R}^n \to \mathbb{R}^n\), og gradienten er derfor en vektorfunktion af samme dimension som inputvektoren \(\boldsymbol x \in \mathbb{R}^n\).

Som eksempel se på gradienten til funktionen \(f: \mathbb{R}^2 \to \mathbb{R}\) med forskriften \(f(\boldsymbol{x}) = 1 - \frac{x_1^2}{2} -\frac{x_2^2}{2}\)

x1, x2 = symbols('x1:3')
f = 1 - x1**2 / 2 - x2**2 / 2

Nabla = dtutools.gradient(f)

f, Nabla

\[\begin{split}\displaystyle \left( - \frac{x_{1}^{2}}{2} - \frac{x_{2}^{2}}{2} + 1, \ \left[\begin{matrix}- x_{1}\\- x_{2}\end{matrix}\right]\right)\end{split}\]

Vi får altså her en vektorfunktionen \(\nabla f: \mathbb R^2 \to \mathbb R^2\) med forskrift \(\nabla f(x_1, x_2) = (-x_1, -x_2)\). I for eksempel punktet \(\boldsymbol x_0 = (1, -1)\) er gradienten:

Nabla.subs({x1: 1, x2: -1})

\[\begin{split}\displaystyle \left[\begin{matrix}-1\\1\end{matrix}\right]\end{split}\]

Retningsafledt af funktion af to variable

Vi betragter igen funktionen \(f: \mathbb{R}^2 \to \mathbb{R}\), med forskriften \(f(\boldsymbol{x}) = 1 - \frac{x_1^2}{2} -\frac{x_2^2}{2}\)

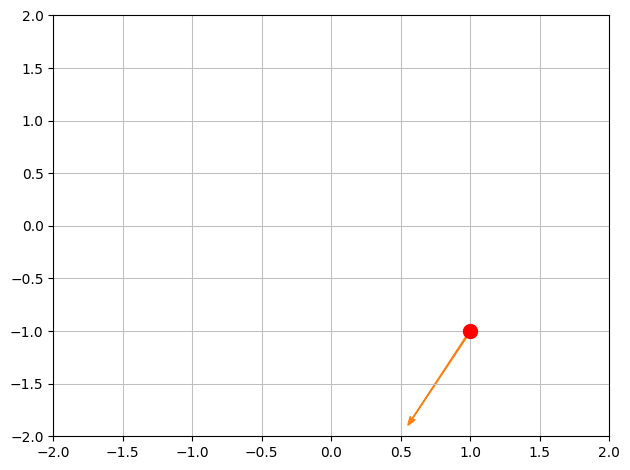
Vi ønsker nu den retningsafledte af \(f\) fra punktet \(\boldsymbol{x_0} = (1,-1)\) i retningen \(\boldsymbol{v} = [-1,-2]^T\):

x0 = Matrix([1,-1])
v = Matrix([-1,-2])
x0, v

\[\begin{split}\displaystyle \left( \left[\begin{matrix}1\\-1\end{matrix}\right], \ \left[\begin{matrix}-1\\-2\end{matrix}\right]\right)\end{split}\]

Vi normaliserer vektoren \(\boldsymbol{v}\) til enhedsvektoren \(\boldsymbol{e}\) givet ved:

e = v.normalized()
e, N(e)

\[\begin{split}\displaystyle \left( \left[\begin{matrix}- \frac{\sqrt{5}}{5}\\- \frac{2 \sqrt{5}}{5}\end{matrix}\right], \ \left[\begin{matrix}-0.447213595499958\\-0.894427190999916\end{matrix}\right]\right)\end{split}\]

p1 = dtuplot.scatter(x0, rendering_kw={"markersize":10,"color":'r'}, xlim=[-2,2],ylim=[-2,2],show=False)
p1.extend(dtuplot.quiver(x0,e,show=False))
p1.show()

Vi får gradienten i punktet \(\boldsymbol{x_0}\) ved

Nabla = Matrix([diff(f,x1),diff(f,x2)]).subs({x1:x0[0],x2:x0[1]})
Nabla

\[\begin{split}\displaystyle \left[\begin{matrix}-1\\1\end{matrix}\right]\end{split}\]

Hvorefter den retningsafledte, \(\nabla_{\boldsymbol{e}} f(\boldsymbol{x_0}) = \braket{\boldsymbol{e},\nabla f(\boldsymbol{x_0})}\) findes ved

a = e.dot(Nabla)
a

Hesse-matricen

Når vi skal bruge et begreb om multivariate (= “af flere varaible”) skalære funktioners krumning (relevant senere for ekstremaanalyse og taylorudvilking), skal vi have gang i anden ordens partielle afledte. Informationen om disse anden ordens afledte samles i hessematricen beskrevet i definition 3.5.1.

Den kan konstrueres manuelt i SymPy fra en given funktion med dens tilhørende anden ordens partielt afledte.

f = 1-x1**2/2-x2**3/2*x3 + x1*x3
f

fx1x1 = f.diff(x1,2)
fx1x2 = f.diff(x1,x2)
fx1x3 = f.diff(x1,x3)
fx2x2 = f.diff(x2,2)
fx2x3 = f.diff(x2,x3)
fx3x3 = f.diff(x3,2)

H1 = Matrix([
    [fx1x1, fx1x2, fx1x3],
    [fx1x2, fx2x2, fx2x3],
    [fx1x3, fx2x3, fx3x3]
])

H1

\[\begin{split}\displaystyle \left[\begin{matrix}-1 & 0 & 1\\0 & - 3 x_{2} x_{3} & - \frac{3 x_{2}^{2}}{2}\\1 & - \frac{3 x_{2}^{2}}{2} & 0\end{matrix}\right]\end{split}\]

Eller selvfølgelig med \(\verb|dtumathtools|\) indbyggede værktøj

H2 = dtutools.hessian(f)
H2

\[\begin{split}\displaystyle \left[\begin{matrix}-1 & 0 & 1\\0 & - 3 x_{2} x_{3} & - \frac{3 x_{2}^{2}}{2}\\1 & - \frac{3 x_{2}^{2}}{2} & 0\end{matrix}\right]\end{split}\]

Hvor punkter i begge tilfælde skal indsættes via \(\verb|.subs()|\)

H1.subs({x1:1,x2:2,x3:3}), H2.subs({x1:1,x2:2,x3:3})

\[\begin{split}\displaystyle \left( \left[\begin{matrix}-1 & 0 & 1\\0 & -18 & -6\\1 & -6 & 0\end{matrix}\right], \ \left[\begin{matrix}-1 & 0 & 1\\0 & -18 & -6\\1 & -6 & 0\end{matrix}\right]\right)\end{split}\]

Jacobi-matricen

Definition 3.8.1 tillader at vi også kan differentiere multivariate vektorfunktioner i form af Jacobi-matricen. For at illustrere dette, definerer vi funktionen \(\boldsymbol f: \mathbb{R}^4 \to \mathbb{R}^3\):

\[\begin{split} \boldsymbol f (\boldsymbol x) = \begin{bmatrix} f_1(\boldsymbol x)\\ f_2(\boldsymbol x)\\ f_3(\boldsymbol x) \end{bmatrix} = \left[\begin{matrix}x_{1}^{2} + x_{2}^{2} x_{3}^{2} + x_{4}^{2} - 1\\x_{1} + \frac{x_{2}^{2}}{2} - x_{3} x_{4}\\x_{1} x_{3} + x_{2} x_{4}\end{matrix}\right] \end{split}\]

x1,x2,x3,x4 = symbols('x1:5', real = True)

f = Matrix([
    x1**2 + x2**2 * x3**2 + x4**2 - 1,
    x1 + x2**2/2 - x3 * x4,
    x1 * x3 + x2 * x4
])

f

\[\begin{split}\displaystyle \left[\begin{matrix}x_{1}^{2} + x_{2}^{2} x_{3}^{2} + x_{4}^{2} - 1\\x_{1} + \frac{x_{2}^{2}}{2} - x_{3} x_{4}\\x_{1} x_{3} + x_{2} x_{4}\end{matrix}\right]\end{split}\]

Bemærk at \(f_1, f_2, f_3\) er differentiable for alle \(\boldsymbol x \in \mathbb{R}^4\), og vi kan derfor bestemme Jacobi-matricen på formen $\( \boldsymbol J_f = \begin{bmatrix} \nabla f_1^T \\ \nabla f_2^T \\ \nabla f_3^T \end{bmatrix} \)$

Dette kan gøres manuelt:

J_f = Matrix.vstack(dtutools.gradient(f[0]).T, dtutools.gradient(f[1]).T, dtutools.gradient(f[2]).T)
J_f

\[\begin{split}\displaystyle \left[\begin{matrix}2 x_{1} & 2 x_{2} x_{3}^{2} & 2 x_{2}^{2} x_{3} & 2 x_{4}\\1 & x_{2} & - x_{4} & - x_{3}\\x_{3} & x_{4} & x_{1} & x_{2}\end{matrix}\right]\end{split}\]

Det kan også gøres således med Sympy’s jacobian:

J = f.jacobian([x1,x2,x3,x4])
J

\[\begin{split}\displaystyle \left[\begin{matrix}2 x_{1} & 2 x_{2} x_{3}^{2} & 2 x_{2}^{2} x_{3} & 2 x_{4}\\1 & x_{2} & - x_{4} & - x_{3}\\x_{3} & x_{4} & x_{1} & x_{2}\end{matrix}\right]\end{split}\]

Parameterkurve i (x,y)-planen og dens tangenter

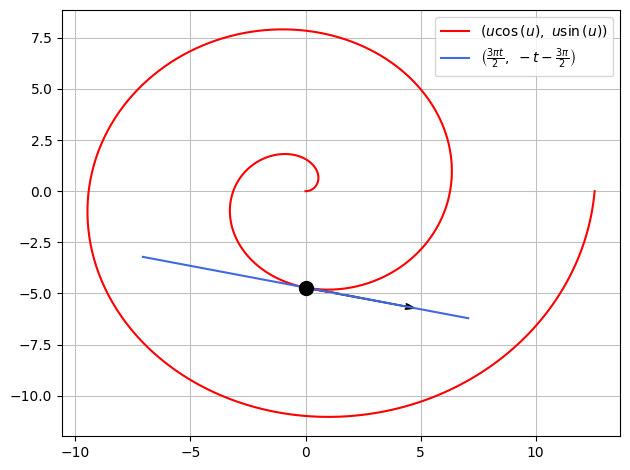
Vi betragter spiralen, givet ved parameterfremstillingen,

u, t = symbols('u t', real=True)
r = Matrix([u*cos(u), u*sin(u)])
r

\[\begin{split}\displaystyle \left[\begin{matrix}u \cos{\left(u \right)}\\u \sin{\left(u \right)}\end{matrix}\right]\end{split}\]

Tangentvektoren i et vilkårligt punkt fåes nu til

rd = diff(r,u)
rd

\[\begin{split}\displaystyle \left[\begin{matrix}- u \sin{\left(u \right)} + \cos{\left(u \right)}\\u \cos{\left(u \right)} + \sin{\left(u \right)}\end{matrix}\right]\end{split}\]

Vi finder nu en parameterfremstilling for tangenten til spiralen i røringspunktet \(((0,-\frac{3\pi}{2}))\), svarende til parameterværdien \(u_0=\frac{3\pi}{2}\), som ses ved,

u0 = 3*pi/2
rdu0 = rd.subs(u,u0)
ru0 = r.subs(u,u0)
ru0

\[\begin{split}\displaystyle \left[\begin{matrix}0\\- \frac{3 \pi}{2}\end{matrix}\right]\end{split}\]

Parameterfremstillingen for tangenten i \(u_0\) findes ved

T = ru0 + t*rdu0
T

\[\begin{split}\displaystyle \left[\begin{matrix}\frac{3 \pi t}{2}\\- t - \frac{3 \pi}{2}\end{matrix}\right]\end{split}\]

Det hele kan nu visualiseres ved

p = dtuplot.plot_parametric(r[0], r[1],(u,0,4*pi),rendering_kw={"color":"red"},use_cm=False,show=False)
p.extend(dtuplot.plot_parametric(T[0],T[1],(t,-1.5,1.5),rendering_kw={"color":"royalblue"},use_cm=False,show=False))
p.extend(dtuplot.scatter(ru0,rendering_kw={"markersize":10,"color":'black'}, show=False))
p.extend(dtuplot.quiver(ru0,rdu0,rendering_kw={"color":"black"},show=False))
p.xlim = [-11,15]
p.ylim = [-12,9]

p.show()