Uge 3: Indre produkt og Norm

Demo af Magnus Troen

from sympy import*
from dtumathtools import*
init_printing()

Indre produkt i SymPy

Det sædvanlige indre produkt \(\left<\cdot, \cdot \right>\) i \(\mathbb{F}^n\) er givet ved:

\[ \left<\cdot, \cdot \right>: V \times V \to \mathbb{F},\quad \left<\boldsymbol{x}, \boldsymbol{y} \right> = \sum_{k=1}^{n} x_k\overline{y}_k, \]

For alle \(\boldsymbol{x},\boldsymbol{y} \in V\). Normen på \(\mathbb{F}^n\) er givet ud fra det indre produkt ved formlen \(\Vert \boldsymbol{x} \Vert = \sqrt{\left<\boldsymbol{x}, \boldsymbol{x} \right>}\). Normen af en vektor er et reelt tal, der ikke er negativt, og det kan udregnes ved:

\[ \Vert \cdot \Vert: V \to \mathbb{R}, \quad \Vert \boldsymbol{x} \Vert = \left(\sum_{k=1}^{n} |x_k|^2 \right)^{1/2} \]

Denne norm har mange navne: den euklidiske norm, \(2\)-normen, \(\ell^2\)-normen. Vi bruger denne medmindre andet nævnes.

Dette kan også opnås i SymPy med kommandoerne hhv. \(\verb|x.dot(y, conjugate_convention = 'right')|\) og \(\verb|x.norm(2)|\) eller bare \(\verb|x.norm()|\).

For ikke at skulle skrive så meget hver gang vi vil bruge et indre produkt definerer vi nu funktionen inner:

def inner(x1: Matrix,x2: Matrix):
    '''
    Computes the inner product of two vectors of same length.
    '''
    
    return x1.dot(x2, conjugate_convention = 'right')

MutableDenseMatrix.inner = inner
ImmutableDenseMatrix.inner = inner

Vi kan nu teste at funktionen virker som forventet:

Vi prøver med vektorerne

\[\begin{split} \pmb{x} = \left[\begin{matrix}1\\2\end{matrix}\right], \pmb{y} = \left[\begin{matrix}2 - i\\2\end{matrix}\right] \end{split}\]

\[ \left<\pmb{x},\pmb{y} \right> = 1\cdot(\overline{2-i}) + 2\cdot \overline{2} = 2+i + 4= 6 + i. \]

x = Matrix([1, 2])
y = Matrix([2-I, 2])

x.inner(y), inner(x,y), y.inner(x), inner(y,x)

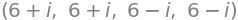
Som forventet.

x.dot(y) udregner prik-produktet, som kendt fra gymnasiet, uden kompleks konjugering, altså \(\boldsymbol{x} \cdot \boldsymbol{y} = \sum_{k=1}^{n} x_k {y}_k\). Hvad sker der hvis vi glemmer conjugate_convention = 'right'? Et problem er at sqrt(x.dot(x)) som skal være en norm ikke nødvendigvis bliver et positivt tal, som vi ville forvente af en længde:

sqrt(y.dot(y)).simplify()

Mens normen af \(\pmb{y}\) skal udregnes ved:

sqrt(inner(y,y)).simplify(), y.norm(), y.norm(2)

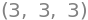
Projektion på linjen

Lad \(\boldsymbol{x}, \boldsymbol{y} \in \mathbb{F}^n\), da vil projektionen af \(\boldsymbol{x}\) på linjen \(Y = \mathrm{span}\{\boldsymbol{y}\}\) kunne opnås med

\[ \operatorname{Proj}_Y(\boldsymbol{x}) = \frac{\left<\boldsymbol{x},\boldsymbol{y} \right>}{\left<\boldsymbol{y},\boldsymbol{y} \right>}\boldsymbol{y} = \left<\boldsymbol{x},\boldsymbol{u}\right>\boldsymbol{u}, \]

hvor \(\boldsymbol{u} = \frac{\boldsymbol{y}}{||\boldsymbol{y}||}\).

Eksempel i \(\mathbb{R}^2\)

Lad først \(\boldsymbol{x}_1, \boldsymbol{x}_2 \in \mathbb{R}^2\), være givet ved:

\[\begin{split} \boldsymbol{x}_1 = \begin{bmatrix} 3\\6\end{bmatrix}, \boldsymbol{x}_2 = \begin{bmatrix} 2\\1\end{bmatrix}. \end{split}\]

Vi ønsker at projektere \(\boldsymbol{x}_1\) ned på linjen givet ved \(X_2 = \mathrm{span}\{\boldsymbol{x}_2\}\)

x1 = Matrix([3,6])
x2 = Matrix([2,1])

projX2_x1 = x1.inner(x2)/x2.inner(x2) * x2 # inner(x1,x2)/x2.norm()**2 * x2
projX2_x1

\[\begin{split}\displaystyle \left[\begin{matrix}\frac{24}{5}\\\frac{12}{5}\end{matrix}\right]\end{split}\]

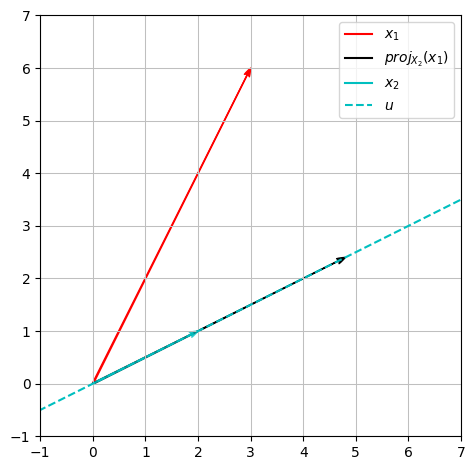
Da vi arbejder med \(\mathbb{R}^2\) kan dette illustreres:

x = symbols('x')
plot_x1 = dtuplot.quiver((0,0),x1,rendering_kw={'color':'r', 'label': '$x_1$'}, xlim = (-1,7), ylim = (-1,7), show = False, aspect='equal')
plot_x2 = dtuplot.quiver((0,0),x2,rendering_kw={'color':'c', 'label': '$x_2$', 'alpha': 0.7}, show = False)
plot_projX2 = dtuplot.quiver((0,0),projX2_x1,rendering_kw={'color':'k', 'label': '$proj_{X_2}(x_1)$'},show = False)
plot_X2 = dtuplot.plot(x2[1]/x2[0] * x, label = '$u$',rendering_kw={'color':'c', 'linestyle': '--'}, legend = True,show = False)

(plot_x1 + plot_X2 + plot_projX2 + plot_x2).show()

Eksempel i \(\mathbb{C}^4\) via lineær afbildning

Først definerer vi vektorerne

c1 = Matrix([2+I, 3, 5-I, 6])
c2 = Matrix([1, I, 3-I, 2])
u = simplify(c2/c2.norm())
c1,c2,u

\[\begin{split}\displaystyle \left( \left[\begin{matrix}2 + i\\3\\5 - i\\6\end{matrix}\right], \ \left[\begin{matrix}1\\i\\3 - i\\2\end{matrix}\right], \ \left[\begin{matrix}\frac{1}{4}\\\frac{i}{4}\\\frac{3}{4} - \frac{i}{4}\\\frac{1}{2}\end{matrix}\right]\right)\end{split}\]

Nu kan projektionen \(\mathrm{Proj}_{\boldsymbol{c}_2}\) beskrives ved den lineære afbildning:

\[ \boldsymbol{P}: \mathbb{C}^4 \to \mathbb{C}^4, \phantom{...} \boldsymbol{P}(\boldsymbol{c}_1) = \boldsymbol{u}\boldsymbol{u}^* \boldsymbol{c_1} \]

hvor \(\boldsymbol{u} = \boldsymbol{c_2}/||\boldsymbol{c_2}||_2\)

P = expand(u*u.adjoint())
P

\[\begin{split}\displaystyle \left[\begin{matrix}\frac{1}{16} & - \frac{i}{16} & \frac{3}{16} + \frac{i}{16} & \frac{1}{8}\\\frac{i}{16} & \frac{1}{16} & - \frac{1}{16} + \frac{3 i}{16} & \frac{i}{8}\\\frac{3}{16} - \frac{i}{16} & - \frac{1}{16} - \frac{3 i}{16} & \frac{5}{8} & \frac{3}{8} - \frac{i}{8}\\\frac{1}{8} & - \frac{i}{8} & \frac{3}{8} + \frac{i}{8} & \frac{1}{4}\end{matrix}\right]\end{split}\]

simplify(P*c1)

\[\begin{split}\displaystyle \left[\begin{matrix}\frac{15}{8}\\\frac{15 i}{8}\\\frac{45}{8} - \frac{15 i}{8}\\\frac{15}{4}\end{matrix}\right]\end{split}\]

Vi kan kontrollere at dette giver det samme forrige metode:

simplify(P*c1 - c1.inner(u)/u.inner(u)*u)

\[\begin{split}\displaystyle \left[\begin{matrix}0\\0\\0\\0\end{matrix}\right]\end{split}\]

Projektionen af \(\pmb{c}_2\) ned på udspændingen af \(\pmb{c}_2\) bør ikke ændre på vektoren \(\pmb{c}_2\). Las os tjekke dette:

P*c2

\[\begin{split}\displaystyle \left[\begin{matrix}\frac{3}{8} + \left(\frac{3}{16} + \frac{i}{16}\right) \left(3 - i\right)\\\frac{3 i}{8} + \left(- \frac{1}{16} + \frac{3 i}{16}\right) \left(3 - i\right)\\\frac{45}{16} - \frac{15 i}{16} + i \left(- \frac{1}{16} - \frac{3 i}{16}\right)\\\frac{3}{4} + \left(\frac{3}{8} + \frac{i}{8}\right) \left(3 - i\right)\end{matrix}\right]\end{split}\]

Det ser umiddelbart ikke så godt ud. Men der er heldigvis hjælp at hente, da vi kan simplificere udtrykket i SymPy:

simplify(P*c2), c2

\[\begin{split}\displaystyle \left( \left[\begin{matrix}1\\i\\3 - i\\2\end{matrix}\right], \ \left[\begin{matrix}1\\i\\3 - i\\2\end{matrix}\right]\right)\end{split}\]

Matricen \(\boldsymbol{P}\) er pr definition hermitisk altså er \(\boldsymbol{P} = \boldsymbol{P}^*\), dette kan testes ved:

P.is_hermitian

True

Eller

simplify(P-P.adjoint())

\[\begin{split}\displaystyle \left[\begin{matrix}0 & 0 & 0 & 0\\0 & 0 & 0 & 0\\0 & 0 & 0 & 0\\0 & 0 & 0 & 0\end{matrix}\right]\end{split}\]

Ortonormale baser

Ortonormale baser viser sig at være vildt praktiske. Det er for eksempel meget nemmere at finde koordinatvektorer med ortonormale baser.

Lad for eksempel

\[\begin{split} \beta = (\boldsymbol{u}_1,\boldsymbol{u}_2,\boldsymbol{u}_3 ) = \left( \left[\begin{matrix}\frac{\sqrt{3}}{3}\\\frac{\sqrt{3}}{3}\\\frac{\sqrt{3}}{3}\end{matrix}\right], \left[\begin{matrix}\frac{\sqrt{2}}{2}\\0\\- \frac{\sqrt{2}}{2}\end{matrix}\right], \left[\begin{matrix}- \frac{\sqrt{6}}{6}\\\frac{\sqrt{6}}{3}\\- \frac{\sqrt{6}}{6}\end{matrix}\right] \right ) \end{split}\]

være en ortonormal basis for \(\mathbb{R}^3\). Nu kan koordinatvektoren \(\phantom{ }_\beta\boldsymbol{x}\) findes ved

\[\begin{split} \phantom{ }_\beta\boldsymbol{x} = \begin{bmatrix} \left<\boldsymbol{u}_1, \boldsymbol{x} \right>\\ \left<\boldsymbol{u}_2, \boldsymbol{x} \right>\\ \left<\boldsymbol{u}_3, \boldsymbol{x} \right> \end{bmatrix} \end{split}\]

for alle \(\boldsymbol{x} \in \mathbb{R}^3\) (sammenlign med Mat1a hvor vi skulle løse et lineært ligningssystem for at finde koordinatvektorer.)

Vi kan starte med at overbevise os selv om at \(\beta\) er en ortonormal basis for \(\mathbb{R}^3\). Først of fremmest skal \(\boldsymbol{u}_1, \boldsymbol{u}_2,\boldsymbol{u}_3\) være ortonormale, hvilket kan vises ved at:

\[\begin{split} \left< \boldsymbol{u}_i, \boldsymbol{u}_j\right> = \begin{cases} 0 & i \neq j\\ 1 & i = j\end{cases},\phantom{...} i,j = 1,2,3 \end{split}\]

u1 = Matrix([sqrt(3)/3, sqrt(3)/3, sqrt(3)/3])
u2 = Matrix([sqrt(2)/2, 0, -sqrt(2)/2])
u3 = Matrix([[-sqrt(6)/6], [sqrt(6)/3], [-sqrt(6)/6]])

u1.inner(u1), u1.inner(u2), u1.inner(u3), u2.inner(u2), u2.inner(u3), u3.inner(u3) 

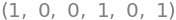
Dette viser at \(\beta\) består af 3 ortonormale vektorer. Da ortonormale vektorer er lineært uafhængige, er vektorerne i \(\beta\) lineært uafhængige. Men 3 lineært uafhængige vektorer i \(\mathbb{R}^3\) udspænder \(\mathbb{R}^3\), så vi konkluderer at \(\beta\) er en ortonormal basis for \(\mathbb{R}^3\).

Vi kan for eksempel nu finde \(\boldsymbol{x} = [1,2,3]\) ‘s koordinatvektor i \(\beta\)-basen.

x = Matrix([1,2,3])
beta_x = Matrix([x.inner(u1) , x.inner(u2) , x.inner(u3)])
beta_x

\[\begin{split}\displaystyle \left[\begin{matrix}2 \sqrt{3}\\- \sqrt{2}\\0\end{matrix}\right]\end{split}\]

Gram-Schmidt algoritmen

Vi har fået give en liste af vektorer \(\gamma = v_1,v_2,v_3,v_4\) for \(\mathbb{C}^4\), hvor

\[\begin{split} \boldsymbol{v}_1 = \left[\begin{matrix}2 i\\0\\0\\0\end{matrix}\right], \: \boldsymbol{v}_2 = \left[\begin{matrix}i\\1\\1\\0\end{matrix}\right], \: \boldsymbol{v}_3 = \left[\begin{matrix}0\\i\\1\\1\end{matrix}\right], \: \boldsymbol{v}_4 = \left[\begin{matrix}0\\0\\0\\i\end{matrix}\right]. \end{split}\]

Vi ønsker at fremstille en ortonormal basis ud fra listen \(\gamma\) ved hjælp af Gram-Schmidt algoritmen.

v1 = Matrix([2*I,0,0, 0])
v2 = Matrix([I, 1, 1, 0])
v3 = Matrix([0, I, 1, 1])
v4 = Matrix([0, 0, 0, I])

Vi skal først kontrollere at vektorene udgører en basis for \(\mathbb{C}^4\):

# vi skal bruge 4 lineært uafhængige vektorer for at danne en basis for C^4
V = Matrix.hstack(v1,v2,v3,v4)
V.rref(pivots=False)

\[\begin{split}\displaystyle \left[\begin{matrix}1 & 0 & 0 & 0\\0 & 1 & 0 & 0\\0 & 0 & 1 & 0\\0 & 0 & 0 & 1\end{matrix}\right]\end{split}\]

Rangen er altå 4, så dette er ok.

Først sættes \(\boldsymbol{w}_1 = \boldsymbol{v}_1\) og \(\boldsymbol{u}_1\) findes ved at normalisere \(\boldsymbol{w}_1\):

w1 = v1
u1 = w1/w1.norm()
u1

\[\begin{split}\displaystyle \left[\begin{matrix}i\\0\\0\\0\end{matrix}\right]\end{split}\]

Nu findes de resterende ortonormale vektorer ved:

i) $\( \boldsymbol{w}_k = \boldsymbol{v}_k - \sum_{j = 1}^{k-1}\left<\boldsymbol{v}_k, \boldsymbol{u}_j\right>\boldsymbol{u}_j \)$

ii) $\( \boldsymbol{u}_k = \frac{\boldsymbol{w}_k}{||\boldsymbol{w}_k||} \)$

w2 = simplify(v2 - v2.inner(u1)*u1)
u2 = expand(w2/w2.norm())

w3 = simplify(v3 - v3.inner(u1)*u1 - v3.inner(u2)*u2)
u3 = expand(w3/w3.norm())

w4 = simplify(v4 - v4.inner(u1)*u1 - v4.inner(u2)*u2 - v4.inner(u3)*u3)
u4 = expand(w4/w4.norm())

u1,u2,u3,u4

\[\begin{split}\displaystyle \left( \left[\begin{matrix}i\\0\\0\\0\end{matrix}\right], \ \left[\begin{matrix}0\\\frac{\sqrt{2}}{2}\\\frac{\sqrt{2}}{2}\\0\end{matrix}\right], \ \left[\begin{matrix}0\\- \frac{\sqrt{2}}{4} + \frac{\sqrt{2} i}{4}\\\frac{\sqrt{2}}{4} - \frac{\sqrt{2} i}{4}\\\frac{\sqrt{2}}{2}\end{matrix}\right], \ \left[\begin{matrix}0\\\frac{\sqrt{2}}{4} + \frac{\sqrt{2} i}{4}\\- \frac{\sqrt{2}}{4} - \frac{\sqrt{2} i}{4}\\\frac{\sqrt{2} i}{2}\end{matrix}\right]\right)\end{split}\]

Det overlades til læseren selv at kontrolere at \(\boldsymbol{u}_1,\boldsymbol{u}_2,\boldsymbol{u}_3,\boldsymbol{u}_4\) er ortonormale:

simplify(u1.inner(u2)) # og så videre

Den nye ortonormal basis \(\boldsymbol{u}_1,\boldsymbol{u}_2,\boldsymbol{u}_3,\boldsymbol{u}_4\) opfylder

\[ \mathrm{ ½}\left\{\boldsymbol{u}_1\right\} = \mathrm{span}\left\{\boldsymbol{v}_1 \right\}. \]

\[ \mathrm{span}\left\{\boldsymbol{u}_1,\boldsymbol{u}_2\right\} = \mathrm{span}\left\{\boldsymbol{v}_1,\boldsymbol{v}_2\right\}. \]

\[ \mathrm{span}\left\{\boldsymbol{u}_1,\boldsymbol{u}_2,\boldsymbol{u}_3\right\} = \mathrm{span}\left\{\boldsymbol{v}_1,\boldsymbol{v}_2,\boldsymbol{v}_3\right\}. \]

og

\[ \mathrm{span}\left\{\boldsymbol{u}_1,\boldsymbol{u}_2,\boldsymbol{u}_3,\boldsymbol{u}_4\right\} = \mathrm{span}\left\{\boldsymbol{v}_1,\boldsymbol{v}_2,\boldsymbol{v}_3,\boldsymbol{v}_4\right\}. \]

Der refereres til beviset for Theorem 2.5.2

Det samme resultat kan opnås med SymPy's indbyggede funktion \(\verb|GramSchimdt|\):

y1,y2,y3,y4 = GramSchmidt([v1,v2,v3,v4], orthonormal=True)
y1,y2,expand(y3),expand(y4)

\[\begin{split}\displaystyle \left( \left[\begin{matrix}i\\0\\0\\0\end{matrix}\right], \ \left[\begin{matrix}0\\\frac{\sqrt{2}}{2}\\\frac{\sqrt{2}}{2}\\0\end{matrix}\right], \ \left[\begin{matrix}0\\- \frac{\sqrt{2}}{4} + \frac{\sqrt{2} i}{4}\\\frac{\sqrt{2}}{4} - \frac{\sqrt{2} i}{4}\\\frac{\sqrt{2}}{2}\end{matrix}\right], \ \left[\begin{matrix}0\\\frac{\sqrt{2}}{4} + \frac{\sqrt{2} i}{4}\\- \frac{\sqrt{2}}{4} - \frac{\sqrt{2} i}{4}\\\frac{\sqrt{2} i}{2}\end{matrix}\right]\right)\end{split}\]

Unitære matricer

Kvadratiske matricer der opfylder kriteriet

\[ \boldsymbol{U}^*\boldsymbol{U} = \boldsymbol{I} \]

kaldes unitære. Sådanne matricer opfylder også \(\boldsymbol{U}\boldsymbol{U}^* = \boldsymbol{I}\).

Hvis \(\boldsymbol{U} \in M_n(\mathbb{R})\) kaldes \(\boldsymbol{U}\) ortogonal (IKKE ortonormal). For ortogonale matricer gælder

\[ \boldsymbol{QQ}^T = \boldsymbol{Q}^T\boldsymbol{Q} = \boldsymbol{I} \]

Reelle, ortogonale matricer er altså automatisk også unitære.

Matricen

\[ \boldsymbol{U} = \left[\boldsymbol{u}_1, \boldsymbol{u}_2, \boldsymbol{u}_3, \boldsymbol{u}_4\right] \]

med u-vektorerne fra Gram-Schmidt er unitær (hvilket gælder generelt når man bruger Gram-Schmidt på \(n\) lineært uafhængige vektorer i \(\mathbb{F}^n\)).

Matricen \(U\) er:

U = Matrix.hstack(u1,u2,u3,u4)
U

\[\begin{split}\displaystyle \left[\begin{matrix}i & 0 & 0 & 0\\0 & \frac{\sqrt{2}}{2} & - \frac{\sqrt{2}}{4} + \frac{\sqrt{2} i}{4} & \frac{\sqrt{2}}{4} + \frac{\sqrt{2} i}{4}\\0 & \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{4} - \frac{\sqrt{2} i}{4} & - \frac{\sqrt{2}}{4} - \frac{\sqrt{2} i}{4}\\0 & 0 & \frac{\sqrt{2}}{2} & \frac{\sqrt{2} i}{2}\end{matrix}\right]\end{split}\]

Det adjungerede (= transponeret og komplekskonjugeret) matrix \(U^*\) af \(U\) er:

U.adjoint(), conjugate(U.T)

\[\begin{split}\displaystyle \left( \left[\begin{matrix}- i & 0 & 0 & 0\\0 & \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} & 0\\0 & - \frac{\sqrt{2}}{4} - \frac{\sqrt{2} i}{4} & \frac{\sqrt{2}}{4} + \frac{\sqrt{2} i}{4} & \frac{\sqrt{2}}{2}\\0 & \frac{\sqrt{2}}{4} - \frac{\sqrt{2} i}{4} & - \frac{\sqrt{2}}{4} + \frac{\sqrt{2} i}{4} & - \frac{\sqrt{2} i}{2}\end{matrix}\right], \ \left[\begin{matrix}- i & 0 & 0 & 0\\0 & \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} & 0\\0 & - \frac{\sqrt{2}}{4} - \frac{\sqrt{2} i}{4} & \frac{\sqrt{2}}{4} + \frac{\sqrt{2} i}{4} & \frac{\sqrt{2}}{2}\\0 & \frac{\sqrt{2}}{4} - \frac{\sqrt{2} i}{4} & - \frac{\sqrt{2}}{4} + \frac{\sqrt{2} i}{4} & - \frac{\sqrt{2} i}{2}\end{matrix}\right]\right)\end{split}\]

At \(U\) er unitær kan tjekkes ved:

simplify(U*U.adjoint()), simplify(U.adjoint()*U)

\[\begin{split}\displaystyle \left( \left[\begin{matrix}1 & 0 & 0 & 0\\0 & 1 & 0 & 0\\0 & 0 & 1 & 0\\0 & 0 & 0 & 1\end{matrix}\right], \ \left[\begin{matrix}1 & 0 & 0 & 0\\0 & 1 & 0 & 0\\0 & 0 & 1 & 0\\0 & 0 & 0 & 1\end{matrix}\right]\right)\end{split}\]