Uge 7: Riemann-Integraler i 1D og 2D

Demo af Karl Johan Funch Måstrup Kristensen, Magnus Troen og Jakob Lemvig

from sympy import *
from dtumathtools import *

init_printing()

I skal nu til at integrere. Og i mange henseender kommer SymPy til være en god hjælp. SymPy’s \(\verb|integrate()|\)-funktion tager hånd om mange integraler, men I vil ofte opleve tidspunkter hvor \(\verb|integrate()|\) har svært ved at knække et integral og I skal udnytte jeres egen viden fra undervisningen til at gøre udtrykket spiseligt for SymPy. Nogen gange trænger SymPy til at få skåret tingene ud i mindre bidder, så den ikke bliver kvalt.

Integration i en dimension

Helt simpelt regnes stamfunktioner i SymPy ved \(\verb|integrate(f, var)|\). \(\verb|var|\) kan udelades i tilfælde hvor funktionen kun har en variabel, men lige så snart der begynder at optræde flere variable (eller symboler defineret med \(\verb|symbols()|\)) skal man definere hvilken variabel man vil integrere efter.

Betragt for eksempel funktionen \(f:\mathbb{R} \to \mathbb{R}\) givet ved

\[\begin{equation*} f(x) = e^x \sin(x) \end{equation*}\]

vi finder stamfunktionen

\[\begin{equation*} F(x) = \int f(x)\; dx = \int e^x \sin(x)\; dx \end{equation*}\]

x = symbols("x", real=True)
f = sqrt(1 - x**2)
f

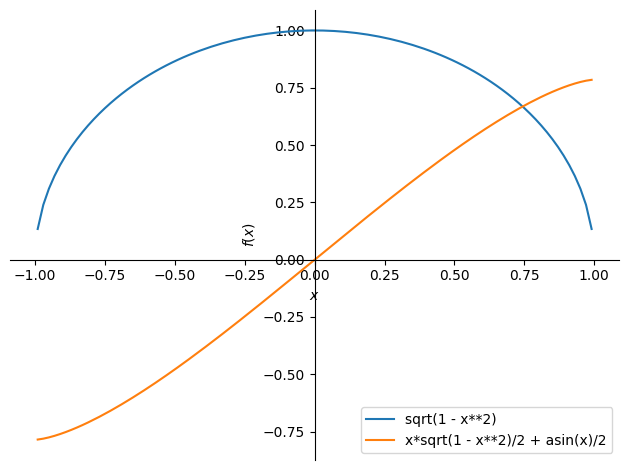
F = integrate(f, x)  # Technically the x is implicit here so integrate(f) would also work
plot(f, F, legend=True)

<sympy.plotting.backends.matplotlibbackend.matplotlib.MatplotlibBackend at 0x7f65d26c2e50>

Bemærk dog at SymPy ikke tilføjer et konstant led efter den har integreret

F

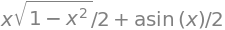
og en konstant skal derfor tilføjes manuelt, hvis man i en opgave bliver bedt om at angive stamfunktionen

C = symbols('C')

F = integrate(f, x) + C
F

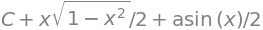
Skal man finde det bestemte integral

\[\begin{equation*} \int_{a}^b f(x)\; dx = F(b) - F(a) \end{equation*}\]

kan gøre brug af stamfunktionen, som vist ovenfor, og/eller få SymPy til det med \(\verb|integrate(f, (var, a, b))|\). Givet for eksempel for Riemann-integralet

\[\begin{equation*} \int_{-1}^1 f(x)\; dx \end{equation*}\]

# Simulated calculation by hand using the fundamental theorem of calculus
display(F.subs(x, 1) - F.subs(x, -1))

# SymPy's integrate function
integrate(f, (x, -1, 1))

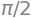
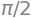
Integration i flere dimensioner

For funktioner af flere variable vil det bestemte integral

\[\begin{equation*} \int\int f(x_1, x_2)\; dx_1 \; dx_2 \end{equation*}\]

kunne findes i SymPy med

integrate(f, x1, x2)

og for bestemte integraler tilføjes grænserne i tuples ligesom i integralet for en dimension

\[\begin{equation*} \int_{a_1}^{b_1}\int_{a_2}^{b_2} f(x_1, x_2)\; dx_1 \; dx_2 \end{equation*}\]

integrate(f, (x1, a1, b1), (x2, a2, b2))

Se eksempelvis på funktionen

x1, x2 = symbols('x1 x2')
f2 = (x1*x2)**3 - x1**2 + sin(3 * x2) + x1*x2**2 + 4
f2

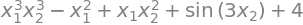
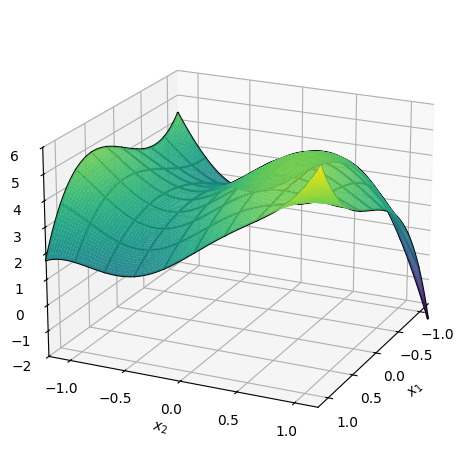
p = dtuplot.plot3d(f2, (x1, -1.2, 1.2), (x2, -1.2, 1.2), zlim=(-2, 6), use_cm=True, colorbar=False,
                   camera = {'azim': 25, 'elev': 20}, wireframe=True, show=False)

p.show()

Stamfunktionen kan findes med

integrate(f2, x1, x2) + C

og et bestemt volume under grafen findes ved det bestemte integral

integrate(f2, (x1, -1.2, 1.2), (x2, -1.2, 1.2))

Tips og tricks til at få Sympy til at integrere

Når SymPy giver problemer med et integral, er der nogle tricks der ofte kan hjælpe.

Definér variable med constraints

Sørg for at angive information om de variable I definerer. Er det for eksempel en reel variabel? Så fortæl det til SymPy. De mest hyppige angivelser er

• real = True

• positive = True

• negative = True

• nonnegative = True

• nonzero = True

Nogle eksempler kunne være:

x1 = symbols('x1', real = True, nonnegative = True) # x1 er reel og ikke-negativ
x2 = symbols('x2', nonzero = True) # x2 er forskellig fra nul

Simplificér før intration

Kald simplify på integranden før der integreres. Dette kan i mange tilfælde nedsætte tiden det kræver at få SymPy til at integrere.

Work flowet bør se sådan ud:

f = 1 / (x1 + x2)

integrand = simplify(f)
F = integrate(integrand, x1, x2)
F

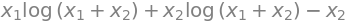
Anvend integralers linearitet

Anvend integralers linearitet. Hvis I skal integrere udtrykket

\[\begin{equation*} \int_{c}^{d}\int_{a}^{b} \alpha f_1(x_1,x_2) + \beta f_2(x_1,x_2) \:dxdy \end{equation*}\]

Vil det ofte være en fordel at arbejde med

\end{equation*} \alpha \int_{c}^d\int_{a}^{b} f_1(x_1,x_2) dxdy + \beta \int_{c}^{d}\int_{a}^{b} f_2(x_1,x_2)dxdy \end{equation*}

Et eksempel kunne være

a = 3
b = 10
c = 2
d = 5
f = S(27)/3 * cos(x1) - 4 * atan(x2 -x1)

integrand1 = simplify(cos(x1)) # Her er det ikke nødvendigt at anvende simplify
integrand2 = simplify(atan(x2 - x1))

F = S(27)/3 * integrate(integrand1, (x1, a,b), (x2, c,d)) - 4 * integrate(integrand2, (x1, a,b), (x2, c,d))
F

Find stamfunktionen først og indsæt grænser bagefter

Nogle gange kan SymPy godt finde en stamfunktion, men ikke evaluere det bestemte integral.

I sådanne tilfælde kan i stedet gøre således

f = tan(ln(x1**2))**3 / x1

integrand = simplify(tan(ln(x1**2))**3)

F = integrate(integrand, (x1,a,b))
F

Vi kan i stedet finde stam funktionen, og selv indsætte grænserne

F = integrate(f, x1)

F.subs(x1, b) - F.subs(x1, a)

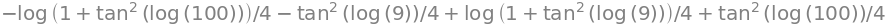
.doit()

Hvis SymPy giver et output hvor integrationen ikke bliver udført, kan man i nogle tilfælde tvinge SymPy til at evaluere integralet med

\[\begin{equation*} \verb|intragte(f, (x,a,b)).doit()| \end{equation*}\]

Man kan dog risikere at dette giver en fejl, og så må man anvende de andre metoder.

Numeriske metoder

Man kan I nogle tilfælde risikere at SymPy enten bruger utrolig lang tid, eller slet ikke kan finde en løsning på et integral, selvom man har hjulpet så meget som man kan. I disse tilfælde kan man blive nødsaget til at løse integralet numerisk. Disse metoder kræver de numeriske libraries numpyog scipy. I har brugt dem i Mat1, Fysik og Programmering, men hvis I ikke har installeret dem, kan det gøres ved:

pip install numpy scipy

eller hvis man bruger pip3

pip3 install numpy scipy

# quad er en numerisk integrator til funktioner af en variabel
# nquad er en numerisk integrator til funktioner af flere variable
from scipy.integrate import quad, nquad
import numpy as np

Her kommer hhv et eksempel på en numerisk løsning i en og to dimensioner.

En dimension

Lad os kigge på integralet

\[\begin{equation*} \int_{\pi}^{10} \frac{\tan^3(\ln(x^2))}{x} dx. \end{equation*}\]

f1 = tan(ln(x**2))**3 / x

# Bemærk: SymPy vil ikke bestemme det begrænsede integral
integrate(f1, (x,pi,10))

Dette er et af de tilfælde hvor SymPy godt kan finde en analytisk løsning, hvis bare vi hjælper lidt, men lad os starte med at løse integralet numerisk.

Først skal vi have konverteret \(f_1\) til en python-/lambdafunktion. Dette gøres med funktionen lambdify og svarer løst sagt til at vi definerer \(f_1\) ved def f1(x):

f1_num = lambdify(x, f1, 'numpy')

# Nu kan vi give f1_num en numerisk værdi og få en numerisk værdi tilbage
f1_num(3)

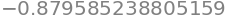
Nu kan quad bruges til at bestemme integralet

F1_num, error1 = quad(f1_num, np.pi, 10)
F1_num, error1

Funktionen quad giver to outputs. Den numeriske approksimation af integralet, og en estimeret fejl (afvigelsen) fra den egentlige løsning.

Vi kan prøve at sammenligne dette med den analytiske løsning. Først kan vi forsøge at tvinge sympy til at evaluere integralet med \(\verb|.doit()|\), men det giver bare en fejl:

# Fjern # for at selv at se fejlen. Maple

# integrate(f1, (x, pi, 10)).doit()

I stedet kan vi få SymPy til at bestemme stamfunktionen, og derefter selv bestemme det bestemte integral

# ad: anti-derivative
F1_ad = integrate(f1, x)
F1_analytic = trigsimp(F1_ad.subs(x,10) - F1_ad.subs(x,pi))
F1_ad, F1_analytic

Lad os sammenligne de to resultater

F1_analytic.evalf() - F1_num

Den numeriske løsning giver altså en god approksimation, men de to resultater er ikke helt ens. Bemærk at den faktiske fejl quad begår er mindre end den estimerede fejl på \(3.4 \cdot 10^{−11}\). Det er jo godt.

To dimensioner

Lad os kigge på udtrykket

\[\begin{equation*} \int_{0}^{\pi}\int_{-10}^{20} \sin(x)\cdot y^2\: dy dx. \end{equation*}\]

Her har SymPy ingen problemer med at finde en løsning, så vi kan let sammenligne den analytiske og numeriske metode.

x,y = symbols('x y', real = True)

f2 = sin(x)*y**2

F2_analytic = integrate(f2, (y,-10,20), (x,0,pi))
F2_analytic

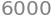
For at evaluere integralet numerisk skal vi igen konvertere \(f_2\), med lambdify.

f2_num = lambdify((x,y), f2, 'numpy')   # lambdify kan tage flere variable

# Nu er f2_num en numerisk funktion af to variable
f2_num(3,4)

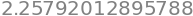
Nu kan integralet bestemmes vha nquad. For en funktion af n variable kaldes nquad ved:

\[\begin{equation*} \verb|nquad(func, [[range for var_1], [range for var_2], ..., [range for var_n]]|) \end{equation*}\]

F2_num, error2 = nquad(f2_num, [[0, np.pi], [-10,20]])
F2_num, error2

De to metode kan nu sammenlignes

F2_num - F2_analytic