Solution of Test Exam (F24)

Suggested Solutions for test exam in 01002/01004 Mathematics 1b, F24.

By shsp@dtu.dk, 05/05-2024

from sympy import *
from dtumathtools import *

init_printing()

Exercise 1

We are given the two partial derivatives, so the following gradient, of a function \(f:\mathbb R^2\to\mathbb R\):

x, y = symbols("x y")
fx = 6 * x - 6 * y
fy = 6 * y**2 - 6 * x
fx, fy

(a)

Setting them equal to zero and solving for all solutions results in all stationary points:

statpt = solve([Eq(fx, 0), Eq(fy, 0)])
statpt

So, \(f\) has the two stationary points, \((0,0)\) and \((1,1)\).

(b)

Second-order partial derivatives:

fxx = diff(fx, x)
fxy = diff(fx, y)
fyx = diff(fy, x)
fyy = diff(fy, y)
fxx, fxy, fyx, fyy

We see that the two partial mixed double derivatives are equal. Since \(f\) also is defined on all of \(\mathbb R^2\), then \(f\) is two-time differentiable (smooth).

The Hessian matrix \(H_f(x,y)\):

H = Lambda(tuple([x, y]), Matrix([[fxx, fxy], [fyx, fyy]]))
H(x, y)

\[\begin{split}\displaystyle \left[\begin{matrix}6 & -6\\-6 & 12 y\end{matrix}\right]\end{split}\]

With no boundary given, extrema can only be found at stationary points or execptional points. Since \(f\) is smooth and defined on all of \(\mathbb R^2\), there are no exceptional points. So, we investigate the eigenvalues of the Hessian matrix at the stationary points:

H(0, 0).eigenvals()

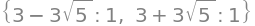
The eigenvalues have different signs, so according to Theorem 5.2.4, \((0,0)\) is a saddel point.

lambdas = H(1, 1).eigenvals(multiple=True)
lambdas[0].evalf(), lambdas[1].evalf()

The eigenvalues are both positive, indicating a local minimum at \((1,1)\).

There are no more possible extremum points, so \(f\) has no maximum.

(c)

We are now informed that \(f(0,0)=1\). For the 2nd-degree Taylor approximating expanded from \(x_0=(0,0)\), we need the 1st-order and 2nd-order partial derivatives evaluated at \((0,0)\):

\[\frac{\partial f(0,0)}{\partial x}=0,\frac{\partial f(0,0)}{\partial y}=0,\frac{\partial^2 f(0,0)}{\partial x^2}=6,\frac{\partial^2 f(0,0)}{\partial y^2}=0,\frac{\partial^2 f(0,0)}{\partial x\partial y}=\frac{\partial^2 f(0,0)}{\partial y\partial x}=-6\]

Setting up the approximation:

\[P_2(x,y)=f(0,0)+\frac{\partial f(0,0)}{\partial x}(x-0)+\frac{\partial f(0,0)}{\partial y}(y-0)+\frac12\frac{\partial^2 f(0,0)}{\partial x^2}(x-0)^2+\frac12\frac{\partial^2 f(0,0)}{\partial y^2}(x-0)^2+\frac{\partial^2 f(0,0)}{\partial x\partial y}(x-0)(y-0)\]

\[=1+0+0+\frac126x^2+0-6xy\]

\[=3x^2-6xy+1\]

Exercise 2

A function \(f:\mathbb R\to \mathbb R\) is given by \(f(0)=1\) and \(f(x)=\sin(x)/x\) when \(x\neq 0\).

(a)

3rd-degree Taylor polynomial of \(\sin(x)\) expanded from \(x_0=0\):

sin(x).series(x, 0, 4)

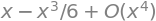
So, the Taylor polynomial of degree 3 is \(P_3(x)=x-\frac{x^3}6.\)

P3 = x - x**3 / 6
P3, sin(x).series(x, 0, 4).removeO()

(b)

The Taylor expansion (Taylor’s limit formula) of \(\sin(x)\) is:

\[\sin(x)=x-\frac{x^3}6+\varepsilon(x)x^3\]

where \(\varepsilon(x)\) is an epsilon function.

We find the following limit value:

\[\lim_{x\to 0}\frac{\sin(x)}{x}=\lim_{x\to 0}\frac{x-\frac{x^3}6+\varepsilon(x)x^3}{x}=\lim_{x\to 0}\left(1-\frac{x^2}6+\varepsilon(x)x^2\right)=1.\]

(c)

According to remark to theorem 3.1.1 in the note, \(f\) is continuous in all points in the interval \(\mathbb R \setminus \{0\}\). In (b) we showed that \(\sin(x)/x\) converges towards \(1\) for \(x\to 0\). By the given definition, \(f(0)=1\), and thus \(f(x)\to f(0)\) for \(x\to 0\), so f is also continuous in \(x=0\).

(d)

Defining the function for \(]0,1]:\)

def f(x):
    return sin(x) / x


f(x)

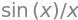
Computing a decimal approximation of \(\int_0^1f(x)\,\mathrm dx\) using SymPy:

integrate(f(x), (x, 0, 1)).evalf()

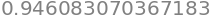
(e)

We will compute a Riemann sum as an approximation of the area under the graph of \(f\) by subdividing the interval \([0,1]\) into \(J=30\) subintervals with equal widths of \(\Delta x_j=1/30\) and finding the right-sum. For such a sum, \(x_j=j/J\) for \(j=1,\ldots,J\):

j = symbols("j")

delta_xj = 1 / 30
J = 30
xj = j / J

Sum(f(xj) * delta_xj, (j, 1, 30)).evalf()

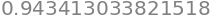
Alternatively, using at for loop:

riemann_sum = 0
N = 30
for i in range(1, N + 1):
    riemann_sum += sin(i / N) / (i / N) * 1 / N

riemann_sum

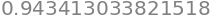
(f)

Computing \(\int_0^1P_3(x)\,\mathrm dx\):

integrate(P3, (x, 0, 1)).evalf()

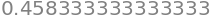
This approximation of the integral is worse than the approximation using a Riemann sum in the previous question, since a Taylor polynomial of \(\sin(x)\) does not approximate \(f\) very well. However, it would have been sensible to use:

integrate(P3 / x, (x, 0, 1)).evalf()

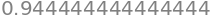
Exercise 3

Given matrix \(C_t\) where \(t\in\mathbb R\):

t = symbols("t")
Ct = Matrix([[1, 2, 3, 4], [4, 1, 2, 3], [3, 4, 1, 2], [t, 3, 4, 1]])
Ct

\[\begin{split}\displaystyle \left[\begin{matrix}1 & 2 & 3 & 4\\4 & 1 & 2 & 3\\3 & 4 & 1 & 2\\t & 3 & 4 & 1\end{matrix}\right]\end{split}\]

(a)

The unitary matrix \(C_t^*\) is the transposed and conjugated matrix. Since \(t\in\mathbb R\), there are no non-real numbers involved, and the conjugation can be ignored. The unitary matrix is thus the transposed matrix, \(C_t^*=C_t^T\):

Ct_uni = Ct.T
Ct_uni

\[\begin{split}\displaystyle \left[\begin{matrix}1 & 4 & 3 & t\\2 & 1 & 4 & 3\\3 & 2 & 1 & 4\\4 & 3 & 2 & 1\end{matrix}\right]\end{split}\]

\(C_t\) is a normal matrix if \(C_tC_t^*=C_t^*C_t,\) so if \(C_tC_t^T=C_t^TC_t\), which is solved for \(t\):

Ct_uni * Ct

\[\begin{split}\displaystyle \left[\begin{matrix}t^{2} + 26 & 3 t + 18 & 4 t + 14 & t + 22\\3 t + 18 & 30 & 24 & 22\\4 t + 14 & 24 & 30 & 24\\t + 22 & 22 & 24 & 30\end{matrix}\right]\end{split}\]

Ct * Ct_uni

\[\begin{split}\displaystyle \left[\begin{matrix}30 & 24 & 22 & t + 22\\24 & 30 & 24 & 4 t + 14\\22 & 24 & 30 & 3 t + 18\\t + 22 & 4 t + 14 & 3 t + 18 & t^{2} + 26\end{matrix}\right]\end{split}\]

solve(Eq(Ct * Ct_uni, Ct_uni * Ct))

So, only for \(t=2\) is \(C_t\) normal.

(b) and (c)

Defining \(A=C_2\):

A = Ct.subs(t, 2)
A

\[\begin{split}\displaystyle \left[\begin{matrix}1 & 2 & 3 & 4\\4 & 1 & 2 & 3\\3 & 4 & 1 & 2\\2 & 3 & 4 & 1\end{matrix}\right]\end{split}\]

Given eigenvectors:

v1 = Matrix([1, 1, 1, 1])
v2 = Matrix([1, I, -1, -I])

Treating \(A\) as a mapping matrix and mapping the eigenvectors:

A * v1, A * v2

\[\begin{split}\displaystyle \left( \left[\begin{matrix}10\\10\\10\\10\end{matrix}\right], \ \left[\begin{matrix}-2 - 2 i\\2 - 2 i\\2 + 2 i\\-2 + 2 i\end{matrix}\right]\right)\end{split}\]

From this we read the scaling factors, which are the eigenvalues corresponding to the given eigenvectors, to be \(\lambda_1=10\) and \(\lambda_2=-2-2i\):

lambda1 = 10
lambda2 = -2 - 2 * I

Check:

A * v1 == lambda1 * v1, A * v2 == simplify(lambda2 * v2)

(True, True)

(d)

Orthogonality is equivalent to an inner product of zero. The inner product of two complex vectors from \(\mathbb C^4\) is a dot product with one vector complex conjugated, \(\langle v_1,v_2\rangle = v_1\cdot \overline{v_2}\):

v1.dot(v2.conjugate())

We conclude that they are orthogonal, \(v_1\perp v_2\).

(e)

The norm is the root of the inner product of a vector with itself, e.g. \(||v_1||=\sqrt{<v_1,v_1>}\). Since \(v_1\in\mathbb R^4\) we can use the usual dot product without conjugation as the inner product for that one. We compute the norms of both eigenvectors:

sqrt(v1.dot(v1))

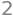
sqrt(v2.dot(v2.conjugate()))

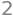
As their norms are not 1, they are not normalized. The list \(v_1,v_2\) is hence orthogonal but not orthonormal.

Exercise 4

Given quadratic form \(q:\mathbb R^2\to\mathbb R\):

def q(x1, x2):
    return 2 * x1**2 - 2 * x1 * x2 + 2 * x2**2 - 4 * x1 + 2 * x2 + 2


x1, x2 = symbols("x1,x2")
q(x1, x2)

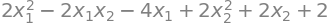
(a)

For rewriting to matrix form \(q(x_1,x_2)=x^TAx+x^Tb+c\), then \(A\), \(b\) and \(c\) can be as follows:

A = Matrix([[2, -1], [-1, 2]])
b = Matrix([-4, 2])
c = 2
A, b, c

\[\begin{split}\displaystyle \left( \left[\begin{matrix}2 & -1\\-1 & 2\end{matrix}\right], \ \left[\begin{matrix}-4\\2\end{matrix}\right], \ 2\right)\end{split}\]

Checking:

x = Matrix([x1, x2])

simplify(list(x.T * A * x + x.T * b)[0] + c)

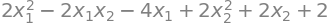
simplify(list(x.T * A * x + x.T * b)[0] + c) == q(x1, x2)

True

(b)

We will now reduce the quadratic form \(q\) to new form called \(q_1\) without “mixed double terms” by changing the basis using an orthogonal change-of-basis matrix \(Q\) that changes from new to original coordinates, meaning \(\tilde x=Q^Tx\). Such \(Q\) consists of orthonormalized eigenvectors of \(A\) as columns.

A.eigenvects()

\[\begin{split}\displaystyle \left[ \left( 1, \ 1, \ \left[ \left[\begin{matrix}1\\1\end{matrix}\right]\right]\right), \ \left( 3, \ 1, \ \left[ \left[\begin{matrix}-1\\1\end{matrix}\right]\right]\right)\right]\end{split}\]

\(A\) has the two linearly independent eigenvectors:

v1 = Matrix([1, 1])
v2 = Matrix([-1, 1])
v1, v2

\[\begin{split}\displaystyle \left( \left[\begin{matrix}1\\1\end{matrix}\right], \ \left[\begin{matrix}-1\\1\end{matrix}\right]\right)\end{split}\]

Also, \(A\) has a corresponding eigenvalue to each eigenvector:

lambda1 = 1
lambda2 = 3
lambda1, lambda2

Since \(A\) is symmetric, then \(v_1\) and \(v_2\) are orthogonal, according to Theorem xx. We normalize them:

q1 = v1.normalized()
q2 = v2.normalized()
q1, q2

\[\begin{split}\displaystyle \left( \left[\begin{matrix}\frac{\sqrt{2}}{2}\\\frac{\sqrt{2}}{2}\end{matrix}\right], \ \left[\begin{matrix}- \frac{\sqrt{2}}{2}\\\frac{\sqrt{2}}{2}\end{matrix}\right]\right)\end{split}\]

A change-of-basis matrix \(Q\) is then:

Q = Matrix.hstack(q1, q2)
Q

\[\begin{split}\displaystyle \left[\begin{matrix}\frac{\sqrt{2}}{2} & - \frac{\sqrt{2}}{2}\\\frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2}\end{matrix}\right]\end{split}\]

This can also be found directly by

Qmat, Lamda = A.diagonalize(normalize=True)
Qmat

\[\begin{split}\displaystyle \left[\begin{matrix}\frac{\sqrt{2}}{2} & - \frac{\sqrt{2}}{2}\\\frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2}\end{matrix}\right]\end{split}\]

(c)

The new coordinates \(\tilde x\) are in code denoted by \(k\):

k1, k2 = symbols("k1 k2")
k = Matrix([k1, k2])
k

\[\begin{split}\displaystyle \left[\begin{matrix}k_{1}\\k_{2}\end{matrix}\right]\end{split}\]

In the new coordinates, the squared terms have coefficients equal to the eigenvalues of \(A\) that correspond to the eigenvectors in \(Q\), which were found above, in the same order. We set up the new form \(q_1\) in the new coordinates, where the original linear terms from \(x^Tb\) are changed to the new basis by performing \(\tilde x^TQ^Tb\):

q1 = lambda1 * k1**2 + lambda2 * k2**2 + list(k.T * Q.T * b)[0] + c
q1

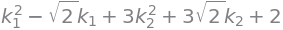
Check:

simplify(list(k.T * Q.T * A * Q * k + k.T * Q.T * b)[0] + c)

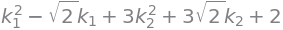
Factorizing by completing the square gives us the following suggestions to the constants:

alpha = 1
gamma = sqrt(2) / 2
beta = 3
delta = -sqrt(2) / 2
alpha, gamma, beta, delta

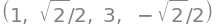
Setting up the suggested factorized form of \(q_1\) to see if it fits:

q1_fact = (
    alpha * (k1 - gamma) ** 2
    - alpha * gamma**2
    + beta * (k2 - delta) ** 2
    - beta * delta**2
    + 2
)
q1_fact

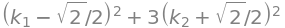
expand(q1_fact)

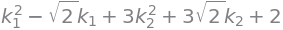
expand(q1_fact) == q1

True

We see that the above listed four constants give us the wanted factorized form from the problem text, which is a correct factorization of \(q_1\).

(d)

We are informed that \(q_1\) in the new coordinates has a stationary point at \((\gamma,\delta)\) with the values of the constants found in (c):

k_statpt = Matrix([gamma, delta])
k_statpt

\[\begin{split}\displaystyle \left[\begin{matrix}\frac{\sqrt{2}}{2}\\- \frac{\sqrt{2}}{2}\end{matrix}\right]\end{split}\]

The point written in the original coordinates:

x_statpt = Q * k_statpt
x_statpt

\[\begin{split}\displaystyle \left[\begin{matrix}1\\0\end{matrix}\right]\end{split}\]

The Hessian matrix of \(q\) is by definition \(H_q=2A\). Since the eigenvalues of \(A\) are positive at all points, then the eigenvalues of \(H_q\) are also positive at all points. Thus, also positive at any stationary points. According to Theorem 5.2.4, if the point \((1,0)\) is a stationary point, then two positive eigenvalues indicate that it is a local minimum.

Exercise 5

Given parametrization of a solid region, for \(u\in[0,1],v\in[0,1],w\in[0,\pi/2]\):

def r(u, v, w):
    return Matrix([v * u**2 * cos(w), v * u**2 * sin(w), u])


u, v, w = symbols("u v w")
r(u, v, w)

\[\begin{split}\displaystyle \left[\begin{matrix}u^{2} v \cos{\left(w \right)}\\u^{2} v \sin{\left(w \right)}\\u\end{matrix}\right]\end{split}\]

We note that \(r\) is injective within the interior of the given parameter intervals.

(a)

Plotting the region:

from sympy.plotting import *

pa = dtuplot.plot3d_parametric_surface(
    *r(u, v, w).subs(v, 1), (u, 0, 1), (w, 0, pi / 2), show=False
)
pb = dtuplot.plot3d_parametric_surface(
    *r(u, v, w).subs(w, pi / 2), (u, 0, 1), (v, 0, 1), show=False
)
pc = dtuplot.plot3d_parametric_surface(
    *r(u, v, w).subs(w, 0), (u, 0, 1), (v, 0, 1), show=False
)
pd = dtuplot.plot3d_parametric_surface(
    *r(u, v, w).subs(u, 1),
    (v, 0, 1),
    (w, 0, pi / 2),
    {"color": "royalblue", "alpha": 0.7},
    show=False
)
(pa + pb + pc + pd).show()

The Jacobian matrix:

Jac_mat = Matrix.hstack(diff(r(u, v, w), u), diff(
    r(u, v, w), v), diff(r(u, v, w), w))
Jac_mat

\[\begin{split}\displaystyle \left[\begin{matrix}2 u v \cos{\left(w \right)} & u^{2} \cos{\left(w \right)} & - u^{2} v \sin{\left(w \right)}\\2 u v \sin{\left(w \right)} & u^{2} \sin{\left(w \right)} & u^{2} v \cos{\left(w \right)}\\1 & 0 & 0\end{matrix}\right]\end{split}\]

The Jacobian determinant:

Jac_det = simplify(Jac_mat.det())
Jac_det

(b)

Given vector field:

x, y, z = symbols("x y z")
V = Matrix([x + exp(y * z), 2 * y - exp(x * z), 3 * z + exp(x * y)])
V

\[\begin{split}\displaystyle \left[\begin{matrix}x + e^{y z}\\2 y - e^{x z}\\3 z + e^{x y}\end{matrix}\right]\end{split}\]

Given function:

f = Lambda(tuple((x, y, z)), diff(V[0], x) + diff(V[1], y) + diff(V[2], z))
f(x, y, z)

(c)

We see above that \(f\) is a constant and thus continuous function. A continuous function satisfying the conditions (I) and (II) on page 140,are guaranteed to be Riemann integrable, according to the remark after definition 6.3.1.

(d)

Since \(r\) is injective and since the Jacobian determinant is non-zero within the interior of the parameter intervals, then we can compute the volume integral of \(f\) over the solid region by integrating along the axis-parallel \(u,v,w\) region and adjusted by the Jacobian function, which is the absolute value of the Jacobian determinant in this case:

integrate(f(*r(u, v, w)) * abs(Jac_det), (u, 0, 1), (v, 0, 1), (w, 0, pi / 2))

Exercise 6

Given elevated surface: \(G=\{(x,y,h(x,y))|0\leq x\leq2,0\leq y\leq1\}\), where \(h\) is given as:

def h(x, y):
    return 2 * x - y + 1


x, y = symbols("x y")
h(x, y)

(a)

Parametrisation of \(G\):

r = Lambda(tuple((u, v)), Matrix([u, v, h(u, v)]))

u, v = symbols("u v")
r(u, v)

\[\begin{split}\displaystyle \left[\begin{matrix}u\\v\\2 u - v + 1\end{matrix}\right]\end{split}\]

wich parameter intervals \(u\in[0,2],v\in[0,1]\). This parametrization is injective in the interior. Plot:

plot3d_parametric_surface(*r(u, v), (u, 0, 2), (v, 0, 1))

<sympy.plotting.backends.matplotlibbackend.matplotlib.MatplotlibBackend at 0x7ff673bce730>

Normal vector to the surface:

N = diff(r(u, v), u).cross(diff(r(u, v), v))
N

\[\begin{split}\displaystyle \left[\begin{matrix}-2\\1\\1\end{matrix}\right]\end{split}\]

The Jacobian function in case of surface integrals is the length (norm) of the normal vector:

Jac = N.norm()
Jac

The area of \(G\) is found as a surface integral of the scalar 1 over the surface. Since \(r\) is injective and the Jacobian function is non-zero on the interior, then we will carry out the surface integral along \(u\) and \(v\) and adjust by the Jacobian:

integrate(Jac, (u, 0, 2), (v, 0, 1))

(b)

The region is now cut in two by a vertical plane through the points \((0,1)\) and \((2,0)\). This cuts the region in the \((x,y)\) plane into two triangles, of which we denote the “lower” triangle by \(\Gamma_1\). Parametrized, where \(u\in[0,2],v\in[0,1]\):

s = Matrix([u, (1 - u/2) * v])
s

\[\begin{split}\displaystyle \left[\begin{matrix}u\\v \left(1 - \frac{u}{2}\right)\end{matrix}\right]\end{split}\]

The elevated surface above \(\Gamma_1\) is denoted \(G_1\). A parametrization of \(G_1\), where \(u\in[0,2],v\in[0,1]\):

r1 = Lambda(tuple((u, v)), Matrix([*s, h(*s)]))
r1(u, v)

\[\begin{split}\displaystyle \left[\begin{matrix}u\\v \left(1 - \frac{u}{2}\right)\\2 u - v \left(1 - \frac{u}{2}\right) + 1\end{matrix}\right]\end{split}\]

Plot:

plot3d_parametric_surface(*r1(u, v), (u, 0, 2), (v, 0, 1))

<sympy.plotting.backends.matplotlibbackend.matplotlib.MatplotlibBackend at 0x7ff67549f580>

Normal vector:

N1 = simplify(diff(r1(u, v), u).cross(diff(r1(u, v), v)))
N1

\[\begin{split}\displaystyle \left[\begin{matrix}u - 2\\1 - \frac{u}{2}\\1 - \frac{u}{2}\end{matrix}\right]\end{split}\]

The Jacobian function:

simplify(N1.norm())

Since \(u\leq2\), we simplify to:

Jac1 = -sqrt(6) * (u - 2)/2
Jac1

(c)

Given function

def f(x, y, z):
    return x + y + z - 1


f(x, y, z)

Surface integral of \(f\) over \(G_1\) is performed over the parameter region since \(r_1\) is injective and the Jacobian function non-zero on the interior of \(\Gamma_1\):

integrate(f(*r1(u, v)) * Jac1, (u, 0, 2), (v, 0, 1))